题目内容
 如图,△ABC的外角平分线CP和内角平分线BP相交于点P,若∠BAC=54°,则∠CAP=
如图,△ABC的外角平分线CP和内角平分线BP相交于点P,若∠BAC=54°,则∠CAP=考点:三角形内角和定理,三角形的外角性质
专题:
分析:过点P作PD⊥AB,PE⊥AC,PF⊥BC,垂足分别为D、E、F,根据角平分线的性质可知PD=PF,PE=PF,故AP是∠DAC的平分线,由此可得出结论.
解答: 解:过点P作PD⊥AB,PE⊥AC,PF⊥BC,垂足分别为D、E、F,
解:过点P作PD⊥AB,PE⊥AC,PF⊥BC,垂足分别为D、E、F,
∵△ABC的外角平分线CP和内角平分线BP相交于点P,
∴PD=PF,PE=PF,
∴PD=PE,
∴AP是∠DAC的平分线.
∴∠BAC=54°,
∴∠CAD=180°-54°=126°,
∴∠CAP=
∠CAD=63°.
故答案为:63°.
 解:过点P作PD⊥AB,PE⊥AC,PF⊥BC,垂足分别为D、E、F,
解:过点P作PD⊥AB,PE⊥AC,PF⊥BC,垂足分别为D、E、F,∵△ABC的外角平分线CP和内角平分线BP相交于点P,
∴PD=PF,PE=PF,
∴PD=PE,
∴AP是∠DAC的平分线.
∴∠BAC=54°,
∴∠CAD=180°-54°=126°,
∴∠CAP=
| 1 |
| 2 |
故答案为:63°.
点评:本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
已知a=2012x+2013,b=2014x+2015,c=2013x+2013,则(2c-a-b)2等于( )
| A、-4 | B、4 | C、-8 | D、8 |
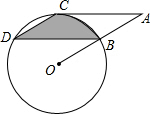 如图,点B、C、D都在⊙O上,过点C作AC∥BD交OB延长线于点A,连接CD,且∠CDB=∠OBD=30°,DB=
如图,点B、C、D都在⊙O上,过点C作AC∥BD交OB延长线于点A,连接CD,且∠CDB=∠OBD=30°,DB=
 如图,⊙O的直径AB和弦CD相交于点E.∠DEB=60°,AE=1,EB=5.试求CD的长.
如图,⊙O的直径AB和弦CD相交于点E.∠DEB=60°,AE=1,EB=5.试求CD的长. 把下列左圈中的每一个整式分别除以
把下列左圈中的每一个整式分别除以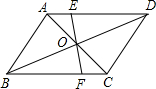 如图,平行四边形ABCD的对角线AC、BD相交于点O,过点O作直线分别交AD、BC于点E、F,如果四边形AEFB的面积为8,则平行四边形ABCD的面积是
如图,平行四边形ABCD的对角线AC、BD相交于点O,过点O作直线分别交AD、BC于点E、F,如果四边形AEFB的面积为8,则平行四边形ABCD的面积是 如图,已知点O是?ABCD的对角线AC,BD的交点,请你添加一个条件使AE=CF,并说明理由.
如图,已知点O是?ABCD的对角线AC,BD的交点,请你添加一个条件使AE=CF,并说明理由. 如图,∠C=90°,∠BAC=30°,BC=1.将直角三角形纸片沿AD折叠,使点C落在AB上的点E处.求tan15°的值.
如图,∠C=90°,∠BAC=30°,BC=1.将直角三角形纸片沿AD折叠,使点C落在AB上的点E处.求tan15°的值.