题目内容
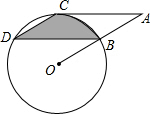 如图,点B、C、D都在⊙O上,过点C作AC∥BD交OB延长线于点A,连接CD,且∠CDB=∠OBD=30°,DB=6
如图,点B、C、D都在⊙O上,过点C作AC∥BD交OB延长线于点A,连接CD,且∠CDB=∠OBD=30°,DB=6| 3 |
(1)直线AC与⊙O有怎样的位置关系?为什么?
(2)求由弦CD、BD与弧BC所围成的阴影部分的面积.(结果保留π)
考点:切线的判定,扇形面积的计算
专题:计算题
分析:(1)连结BC、OD、OC,OC交BD于E,如图,根据圆周角定理得∠BOC=2∠BDC=60°,再根据平行线的性质,由AC∥BD得∠A=∠OBD=30°,则∠ACO=90°,于是根据切线的判定定理即可得到AC为⊙O的切线;
(2)根据平行线的性质,由OC⊥AC,BD∥AC得OC⊥BD,再利用垂径定理得BE=DE=
BD=3
,则利用∠OBE=30°,可计算出OE=
BE=3,OB=2OE=6,接着判断四边形BODC为菱形,得到S△CDE=S△OBE,所以由弦CD、BD与弧BC所围成的阴影部分的面积,然后根据扇形面积公式求解.
(2)根据平行线的性质,由OC⊥AC,BD∥AC得OC⊥BD,再利用垂径定理得BE=DE=
| 1 |
| 2 |
| 3 |
| ||
| 3 |
解答:解:(1)直线AC与⊙O相切.理由如下: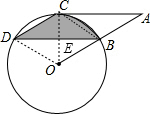
连结BC、OD、OC,OC交BD于E,如图,
∵∠BOC=2∠BDC=2×30°=60°,
∵AC∥BD,
∴∠A=∠OBD=30°,
∴∠ACO=180°-∠A-∠AOC=90°,
∴OC⊥AC,
∴AC为⊙O的切线;
(2)解:∵OC⊥AC,BD∥AC,
∴OC⊥BD,
∴BE=DE=
BD=3
,
∵∠OBE=30°,
∴OE=
BE=3,OB=2OE=6,
∴CE=OE,
∴OC和BD互相垂直平分,
∴四边形BODC为菱形,
∴S△CDE=S△OBE,
∴由弦CD、BD与弧BC所围成的阴影部分的面积=S扇形BOC=
=6π(cm2).

连结BC、OD、OC,OC交BD于E,如图,
∵∠BOC=2∠BDC=2×30°=60°,
∵AC∥BD,
∴∠A=∠OBD=30°,
∴∠ACO=180°-∠A-∠AOC=90°,
∴OC⊥AC,
∴AC为⊙O的切线;
(2)解:∵OC⊥AC,BD∥AC,
∴OC⊥BD,
∴BE=DE=
| 1 |
| 2 |
| 3 |
∵∠OBE=30°,
∴OE=
| ||
| 3 |
∴CE=OE,
∴OC和BD互相垂直平分,
∴四边形BODC为菱形,
∴S△CDE=S△OBE,
∴由弦CD、BD与弧BC所围成的阴影部分的面积=S扇形BOC=
| 60•π•62 |
| 360 |
点评:本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了扇形的计算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,BD=OD,∠AOC=114°,求∠AOD的度数.
如图,BD=OD,∠AOC=114°,求∠AOD的度数. 在平行四边形ABCD的对角线AC上截取AE=CF,作EH⊥BC,FG⊥AD.求证:GH与EF互相平分.
在平行四边形ABCD的对角线AC上截取AE=CF,作EH⊥BC,FG⊥AD.求证:GH与EF互相平分. 如图,梯形ABCD中,AD∥BC,∠ABC+∠BCD=90°,且BC=3AD,分别以BA、AD、DC为边向梯形外作正方形,其面积分别为S1,S2,S3,则S1,S2,S3之间的关系是
如图,梯形ABCD中,AD∥BC,∠ABC+∠BCD=90°,且BC=3AD,分别以BA、AD、DC为边向梯形外作正方形,其面积分别为S1,S2,S3,则S1,S2,S3之间的关系是 已知△ABC,过点C作AB边上的高线CD,过点A作BC边上的高线AE.
已知△ABC,过点C作AB边上的高线CD,过点A作BC边上的高线AE. 如图梯形ABCD中,AD∥BC,E是AB的中点,过点E作EF∥AD,交CD于F.测量AD,BC,EF的长度后,写出这三条线段间的数量关系.
如图梯形ABCD中,AD∥BC,E是AB的中点,过点E作EF∥AD,交CD于F.测量AD,BC,EF的长度后,写出这三条线段间的数量关系. 如图,△ABC的外角平分线CP和内角平分线BP相交于点P,若∠BAC=54°,则∠CAP=
如图,△ABC的外角平分线CP和内角平分线BP相交于点P,若∠BAC=54°,则∠CAP=