题目内容
如图,在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c则a,b,c满足的关系为 .
(1)以直角三角形的三边为边长作正方形,如图①,你能发现这三个正方形的面积之间有什么关系吗?
(2)分别以直角三角形的三边长为直径作半圆,如图②,你能发现这三个半圆的面积之间有什么关系吗?试说明你所发现的结论;
(3)若a=8,b=6,分别以直角三角形三边为直径作半圆(如图③所示)求阴影部分的面积.

(1)以直角三角形的三边为边长作正方形,如图①,你能发现这三个正方形的面积之间有什么关系吗?
(2)分别以直角三角形的三边长为直径作半圆,如图②,你能发现这三个半圆的面积之间有什么关系吗?试说明你所发现的结论;
(3)若a=8,b=6,分别以直角三角形三边为直径作半圆(如图③所示)求阴影部分的面积.

考点:勾股定理
专题:
分析:根据勾股定理即可得到a,b,c满足的关系.
(1)根据正方形的面积公式结合勾股定理就可发现大正方形的面积是两个小正方形的面积和;
(2)分别表示出S1、S2、S3,结合勾股定理即可得出关系式.
(3)根据半圆的面积公式以及勾股定理就可发现:两个小半圆的面积和等于大半圆的面积,从而得出阴影部分的面积=直角三角形的面积.
(1)根据正方形的面积公式结合勾股定理就可发现大正方形的面积是两个小正方形的面积和;
(2)分别表示出S1、S2、S3,结合勾股定理即可得出关系式.
(3)根据半圆的面积公式以及勾股定理就可发现:两个小半圆的面积和等于大半圆的面积,从而得出阴影部分的面积=直角三角形的面积.
解答:解:根据勾股定理可知,a2+b2=c2.
(1)由题意得,S1=b2,S2=a2,S3=c2,
∵a2+b2=c2,
∴S1+S2=S3.
(2)S1=
×b2,S2=
×a2,S3=
×c2,
∵a2+b2=c2,
∴S1+S2=S3.
(3)因为a2+b2=c2,
两边同乘以
,即得两小半圆的面积和等于大半圆的面积,
从而可得S阴影部分的面积=S直角三角形的面积=
×8×6=24.
故阴影部分的面积是24.
故答案为:a2+b2=c2.
(1)由题意得,S1=b2,S2=a2,S3=c2,
∵a2+b2=c2,
∴S1+S2=S3.
(2)S1=
| π |
| 8 |
| π |
| 8 |
| π |
| 8 |
∵a2+b2=c2,
∴S1+S2=S3.
(3)因为a2+b2=c2,
两边同乘以
| π |
| 8 |
从而可得S阴影部分的面积=S直角三角形的面积=
| 1 |
| 2 |
故阴影部分的面积是24.
故答案为:a2+b2=c2.
点评:本题考查了勾股定理、正方形的面积公式及圆的面积公式,解答此类题目关键是仔细观察所给图形的特点,不要盲目作答.

练习册系列答案
相关题目
 在平行四边形ABCD的对角线AC上截取AE=CF,作EH⊥BC,FG⊥AD.求证:GH与EF互相平分.
在平行四边形ABCD的对角线AC上截取AE=CF,作EH⊥BC,FG⊥AD.求证:GH与EF互相平分. 如图梯形ABCD中,AD∥BC,E是AB的中点,过点E作EF∥AD,交CD于F.测量AD,BC,EF的长度后,写出这三条线段间的数量关系.
如图梯形ABCD中,AD∥BC,E是AB的中点,过点E作EF∥AD,交CD于F.测量AD,BC,EF的长度后,写出这三条线段间的数量关系.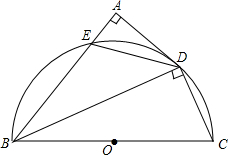 如图,BC为半圆的直径,O为圆心,BC=10,AD与半圆相切于点D,AB交⊙O于点E,DA⊥AB,AD=4
如图,BC为半圆的直径,O为圆心,BC=10,AD与半圆相切于点D,AB交⊙O于点E,DA⊥AB,AD=4  如图,已知∠1=∠2,BD平分∠ABC.
如图,已知∠1=∠2,BD平分∠ABC. 如图,△ABC的外角平分线CP和内角平分线BP相交于点P,若∠BAC=54°,则∠CAP=
如图,△ABC的外角平分线CP和内角平分线BP相交于点P,若∠BAC=54°,则∠CAP= 如图,∠A+∠B+∠C+∠D+∠E=
如图,∠A+∠B+∠C+∠D+∠E=