题目内容
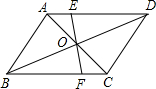如图，平行四边形ABCD的对角线AC、BD相交于点O，过点O作直线分别交AD、BC于点E、F，如果四边形AEFB的面积为8，则平行四边形ABCD的面积是考点：平行四边形的性质
专题：
分析：根据矩形的对称性可以得到四边形AEFB和四边形CFED的面积相等，从而确定结论．
解答：解：∵四边形ABCD是平行四边形，
∴它是一个中心对称图形，对称中心是两对角线的交点，
∵线段EF过点O，
∴四边形AEFB的面积等于四边形CFED的面积，
∵四边形AEFB的面积为8，
∴四边形ABCD的面积为16，
故答案为：16．
∴它是一个中心对称图形，对称中心是两对角线的交点，
∵线段EF过点O，
∴四边形AEFB的面积等于四边形CFED的面积，
∵四边形AEFB的面积为8，
∴四边形ABCD的面积为16，
故答案为：16．
点评：本题考查了平行四边形的性质，解题的关键是了解过平行四边形的对称中心的任一条直线都能将平行四边形的面积分成相等的两部分．
练习册系列答案
名校课堂系列答案
相关题目
如图，已知∠1=∠2，BD平分∠ABC．
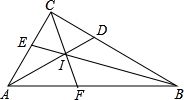如图，在△ABC中，∠ACB=90°，角平分线BE、AD相交于I，连结CI并延长交AB于点F，则下列结论中错误的是（ ）| A、点I在∠ABC的平分线上 |
| B、点F在∠AIB的平分线上 |
| C、∠ACI=45° |
| D、∠CAD+∠ABE+∠BCF=90° |
如图，△ABC的外角平分线CP和内角平分线BP相交于点P，若∠BAC=54°，则∠CAP=下列计算中，正确的是（ ）
| A、-0.12=0.2 |
| B、-|-2|2=4 |
| C、（-3）3=-6 |
| D、-（-1）2n+1=1（n表示自然数） |
如图，在Rt△ABC中，∠ACB=90°，两个正方形面积如图所示，则△ABC的周长是