题目内容
1．
如图，在△ABC中，D、E分别是AB、AC上的点，且DE∥BC，若S△ADE：S△ABC=4：9，则AD：AB=（ ）| A． | 1：2 | B． | 2：3 | C． | 1：3 | D． | 4：9 |
分析 由DE∥BC，即可证得△ADE∽△ABC，又由S△ADE：S△ABC=4：9，根据相似三角形的面积比等于相似比的平方，即可求得答案．
解答 解：∵DE∥BC，
∴△ADE∽△ABC，
∵S△ADE：S△ABC=4：9，
∴AD：AB=2：3．
故选B．
点评 此题考查了相似三角形的判定与性质．注意相似三角形的面积比等于相似比的平方定理的应用．
练习册系列答案
相关题目
11．
教室里的饮水机接通电源就进入自动程序，开机加热时每分钟上升10℃，加热100℃，停止加热，水温开始下降，此时水温（℃）与开机后用时（min）成反比例关系．直至水温降至30℃，饮水机关机．饮水机关机后即刻自动开机，重复上述自动程序．若在水温为30℃时，接通电源后，水温y（℃）和时间（min）的关系如图，为了在上午第一节下课时（8：25）能喝到不小于70℃的水，则接通电源的时间可以是当天上午的（ ）
教室里的饮水机接通电源就进入自动程序，开机加热时每分钟上升10℃，加热100℃，停止加热，水温开始下降，此时水温（℃）与开机后用时（min）成反比例关系．直至水温降至30℃，饮水机关机．饮水机关机后即刻自动开机，重复上述自动程序．若在水温为30℃时，接通电源后，水温y（℃）和时间（min）的关系如图，为了在上午第一节下课时（8：25）能喝到不小于70℃的水，则接通电源的时间可以是当天上午的（ ）| A． | 7：00 | B． | 7：10 | C． | 7：25 | D． | 7：35 |
9．如果一个多边形的内角和是其外角和的两倍，那么这个多边形是（ ）
| A． | 六边形 | B． | 五边形 | C． | 四边形 | D． | 三角形 |
如图，△ABC，用尺规作图作角平分线CD．（保留作图痕迹，不要求写作法）
8．一组数据：5，7，4，9，7的中位数和众数分别是（ ）
| A． | 4，7 | B． | 7，7 | C． | 4，4 | D． | 4，5 |
8．
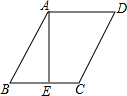如图，在平行四边形ABCD中，AE⊥BC于E，AE=EB=EC=a，且a是一元二次方程x2+2x-3=0的根，则平行四边形ABCD的周长为（ ）
如图，在平行四边形ABCD中，AE⊥BC于E，AE=EB=EC=a，且a是一元二次方程x2+2x-3=0的根，则平行四边形ABCD的周长为（ ）| A． | $12-6\sqrt{2}$ | B． | $6\sqrt{2}+12$ | C． | $4+2\sqrt{2}$ | D． | $4-2\sqrt{2}$ |