题目内容
20. 如图,等腰三角形ABC的周长为21,底边BC的长为5,腰AB的垂直平分线交AB于点D,交AC于点E,连接BE,则三角形BEC的周长为( )
如图,等腰三角形ABC的周长为21,底边BC的长为5,腰AB的垂直平分线交AB于点D,交AC于点E,连接BE,则三角形BEC的周长为( )| A. | 11 | B. | 12 | C. | 13 | D. | 14 |
分析 由等腰三角形ABC的周长为21,底边BC的长为5,可求得腰长,又由腰AB的垂直平分线交AB于点D,交AC于点E,根据线段垂直平分线的性质,可得BE=AE,继而可证得三角形BEC的周长=BC+AC.
解答 解:∵等腰三角形ABC的周长为21,底边BC的长为5,
∴AB=AC=$\frac{1}{2}$×(21-5)=8,
∵DE是腰AB的垂直平分线,
∴AE=BE,
∴三角形BEC的周长为:BC+CE+BE=BC+CE+AE=BC+AC=8+5=13.
故选C.
点评 此题考查了线段垂直平分线的性质以及等腰三角形的性质.注意垂直平分线上任意一点,到线段两端点的距离相等.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
8.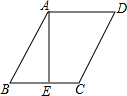 如图,在平行四边形ABCD中,AE⊥BC于E,AE=EB=EC=a,且a是一元二次方程x2+2x-3=0的根,则平行四边形ABCD的周长为( )
如图,在平行四边形ABCD中,AE⊥BC于E,AE=EB=EC=a,且a是一元二次方程x2+2x-3=0的根,则平行四边形ABCD的周长为( )
 如图,在平行四边形ABCD中,AE⊥BC于E,AE=EB=EC=a,且a是一元二次方程x2+2x-3=0的根,则平行四边形ABCD的周长为( )
如图,在平行四边形ABCD中,AE⊥BC于E,AE=EB=EC=a,且a是一元二次方程x2+2x-3=0的根,则平行四边形ABCD的周长为( )| A. | $12-6\sqrt{2}$ | B. | $6\sqrt{2}+12$ | C. | $4+2\sqrt{2}$ | D. | $4-2\sqrt{2}$ |
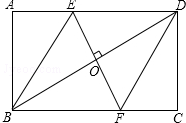 如图,在矩形ABCD中,边AB的长为3,点E,F分别在AD,BC上,连接BE,DF,EF,BD.若四边形BEDF是菱形,且EF=AE+FC,则边BC的长为3$\sqrt{3}$.
如图,在矩形ABCD中,边AB的长为3,点E,F分别在AD,BC上,连接BE,DF,EF,BD.若四边形BEDF是菱形,且EF=AE+FC,则边BC的长为3$\sqrt{3}$.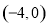 ,B
,B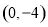 ,C
,C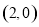 三点.
三点.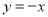 上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.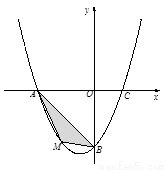
 如图,在Rt△ABC中,∠C=90°,BC=3cm,AC=4cm,那么sinA=$\frac{3}{5}$.
如图,在Rt△ABC中,∠C=90°,BC=3cm,AC=4cm,那么sinA=$\frac{3}{5}$.