题目内容
16.已知二次函数图象经过点A(1,3),B(0,2),C(5,3)三点,求此二次函数解析式.分析 设二次函数解析式为y=ax2+bx+c,利用待定系数法求解即可.
解答 解:设二次函数解析式为y=ax2+bx+c,
根据题意得$\left\{\begin{array}{l}{a+b+c=3}\\{c=2}\\{25a+5b+c=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-\frac{1}{5}}\\{b=\frac{6}{5}}\\{c=2}\end{array}\right.$.
所以二次函数解析式为y=-$\frac{1}{5}$x2+$\frac{6}{5}$x+2.
点评 本题考查了用待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 如图,在15×15的正方形网格中建立平面直角坐标系,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
如图,在15×15的正方形网格中建立平面直角坐标系,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上). 一个装有进水管和出水管的容器,从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分钟)之间的部分关系如图象所示.求从关闭进水管起需要多少分钟该容器内的水恰好放完.
一个装有进水管和出水管的容器,从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分钟)之间的部分关系如图象所示.求从关闭进水管起需要多少分钟该容器内的水恰好放完. 如图,一次函数y=-$\frac{2}{3}$x+$\frac{4}{3}$与x轴交于点A.
如图,一次函数y=-$\frac{2}{3}$x+$\frac{4}{3}$与x轴交于点A.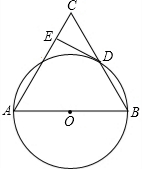 如图,在△ABC中,以AB为直径的⊙O与BC相交于点D,过点D作⊙O的切线交AC于点E.若⊙O的半径为5,∠CDE=20°,则$\widehat{BD}$的长为$\frac{10π}{9}$.
如图,在△ABC中,以AB为直径的⊙O与BC相交于点D,过点D作⊙O的切线交AC于点E.若⊙O的半径为5,∠CDE=20°,则$\widehat{BD}$的长为$\frac{10π}{9}$.