题目内容
6．当x取何值时，代数式-2x2-5x+7的值最大？最大值是多少？分析 把代数式-2x2-5x+7配方成a（x-b）2+c的形式，根据任何数的平方是非负数即可求解．
解答 解：根据题意可设y=-2x2-5x+7，即为求y的最大值，
∵y=-2x2-5x+7=-2（x+$\frac{5}{4}$）2+$\frac{31}{8}$，
根据-2（x+$\frac{5}{4}$）2≤0，可以得到：当x=-$\frac{5}{4}$时，y最大，最大值为$\frac{31}{8}$．
点评 本题考查的是配方法的应用、非负数的性质，掌握配方法的一般步骤、非负数的性质是解题的关键．
练习册系列答案
相关题目
如图，在△ABC中，点D在AB上，点E在AC上，DE∥BC．若∠A=62°，∠AED=54°，则∠B的大小为64°．
如图，P是△ABC两个外角∠DBC与∠ECB平分线的交点，∠A=80°，则∠BPC=50°．
18．关于x，y的二元一次方程（a-1）x+（a+2）y+5-2a=0，当a取一个确定的值时就得到一个方程，所有这些方程有一个公共解，则这个公共解是（ ）
| A． | $\left\{\begin{array}{l}{x=3}\\{y=5}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{x=3}\\{y=-1}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ |
15．
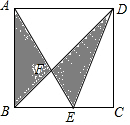如图，正方形ABCD中，E为BC中点，AE、BD交于点F，则阴影部分面积为（ ）
如图，正方形ABCD中，E为BC中点，AE、BD交于点F，则阴影部分面积为（ ）| A． | $\frac{1}{3}$SABCD | B． | $\frac{1}{6}$SABCD | C． | $\frac{1}{2}$SABCD | D． | $\frac{1}{9}$SABCD |