题目内容
11.已知a,b,c为三角形的三边且满足a2+b2+c2=6a+8b+10c-50,试判断三角形的形状.分析 利用一次项的系数分别求出常数项,把50分成9、16、25,然后与(a2-6a)、(b2-8b)、(c2-10c)分别组成完全平方公式,再利用非负数的性质,可分别求出a、b、c的值,然后利用勾股定理逆定理可证△ABC是直角三角形.
解答 解:△ABC是直角三角形
理由:∵a2+b2+c2=6a+8b+10c-50,
∴a2+b2+c2-6a-8b-10c+50=0,
∴a2-6a+9+b2-8b+16+c2-10c+25=0,
即(a-3)2+(b-4)2+(c-5)2=0,
∴a=3,b=4,c=5,
∵32+42=52,
∴△ABC是直角三角形.
点评 本题主要考查了配方法的应用、勾股定理、非负数的性质,解题的关键是注意配方法的步骤,在变形的过程中不要改变式子的值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.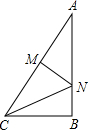 如图,在Rt△ABC中,∠B=90°,AC=10,BC=6,线段AC的垂直平分线MN分别交AC、AB于M、N两点,则CN的长为( )
如图,在Rt△ABC中,∠B=90°,AC=10,BC=6,线段AC的垂直平分线MN分别交AC、AB于M、N两点,则CN的长为( )
 如图,在Rt△ABC中,∠B=90°,AC=10,BC=6,线段AC的垂直平分线MN分别交AC、AB于M、N两点,则CN的长为( )
如图,在Rt△ABC中,∠B=90°,AC=10,BC=6,线段AC的垂直平分线MN分别交AC、AB于M、N两点,则CN的长为( )| A. | $\frac{35}{8}$ | B. | $\frac{25}{4}$ | C. | $\frac{25}{2}$ | D. | 7 |
2.下列事件中,必然事件的是( )
| A. | a是实数,-a2≤0 | |
| B. | 天上打雷后就下雨 | |
| C. | 掷一枚质地均匀的硬币一次,反面朝上 | |
| D. | 某运动员跳高的最好成绩是200.1米 |
20.已知A、B两个动点同时在数轴上匀速运动,且保持运动的方向不变.若A、B两点的起始位置分别用有理数a、b表示,c是最大的负整数,且|a-19c2|+|b-8c3|=0
(1)求a、b、c的值
(2)根据题意及表格中的已知数据,填写完表格:
(3)若A、B两点同时到达点M的位置,且点M用有理数m表示,求m的值
(4)A、B两点能否相距18个单位长度?如果能,求出此时运动了多少秒及此时A、B两点表示的有理数;如果不能,请说明理由.
(1)求a、b、c的值
(2)根据题意及表格中的已知数据,填写完表格:
| 运动时间(秒) | 0 | 5 | 7 | t |
| A点位置 | a | -1 | ||
| B点位置 | b | 17 | 27 |
(4)A、B两点能否相距18个单位长度?如果能,求出此时运动了多少秒及此时A、B两点表示的有理数;如果不能,请说明理由.