题目内容
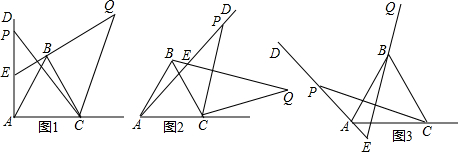
已知甲楼高15米，自甲楼楼顶B处看乙楼楼顶D的仰角为25°，看乙楼楼底C的俯角为40°，现要在两楼楼顶B、D之间拉一横幅，求乙楼的高度CD以及横幅BD的长度．（结果均精确到1米）（参考数据：sin25°≈0.42，tan25°≈0.46，sin40°≈0.64，tan40°≈0.80）
考点：解直角三角形的应用-仰角俯角问题
专题：
分析：过点B作BE⊥CD于点E，解Rt△ABC求出AC，继而得出BE，解Rt△BDE求出DE，BD，继而得出乙楼CD的高度．
解答：解：过点A作AE⊥CD于点E，
在Rt△ABC中，∠ACB=∠EBC=40°，AB=15米，
∵tan∠ACB=
，
∴AC=
=
=18.75米，
∴BE=AC=18.75米，
在Rt△BDE中，∠DBE=25°，
∴DE=BE•tan∠DBE=18.75×0.46=8.625米，BD=
=
≈21米，
∴CD=DE+CE=DE+AB=8.625+15≈24米．
答：乙楼CD的高度约为24米，横幅BD的长度约为21米．
在Rt△ABC中，∠ACB=∠EBC=40°，AB=15米，
∵tan∠ACB=
| AB |
| AC |
∴AC=
| AB |
| tan∠ACB |
| 15 |
| 0.80 |
∴BE=AC=18.75米，
在Rt△BDE中，∠DBE=25°，
∴DE=BE•tan∠DBE=18.75×0.46=8.625米，BD=
| DE |
| sin∠DBE |
| 8.625 |
| 0.42 |
∴CD=DE+CE=DE+AB=8.625+15≈24米．
答：乙楼CD的高度约为24米，横幅BD的长度约为21米．
点评：本题考查了解直角三角形的应用-仰角俯角问题，解答本题的关键是构造直角三角形，要求同学们熟练掌握锐角三角函数的定义．
练习册系列答案
互动英语系列答案
名牌学校分层周周测系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
下列各式中计算正确的是（ ）
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
如图，在△ABC中，∠C=90°，D是AC边上一点，且AD=BD=5，tan∠CBD=
如图，Rt△ABC中，分别以AB、AC为斜边，向△ABC的内侧作等腰Rt△ABE、Rt△ACD，点M是BC的中点，连接MD、ME．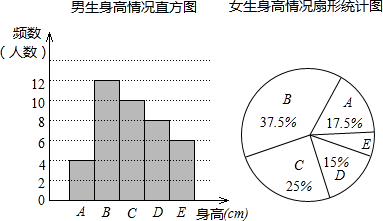
抽样检查，已知抽取的样本中，男生女生的人数相同，利用所得数据绘制如下统计图表：