题目内容
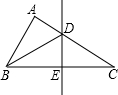 如图,在△ABC中,BC边上的垂直平分线交AC于点D,
如图,在△ABC中,BC边上的垂直平分线交AC于点D,①由垂直平分线定义得到:BE=
②还可得到:BD=DC,理由是:
③已知,AB=3,AC=7,BC=8,则△ABD的周长为
考点:线段垂直平分线的性质
专题:
分析:①根据线段垂直平分线的定义可直接得到;
②根据线段垂直平分线的性质可得到;
③根据△ABD的周长=AB+AC可得出.
②根据线段垂直平分线的性质可得到;
③根据△ABD的周长=AB+AC可得出.
解答:解:①∵DE是线段BC的中垂线,
∴BE=CE,DE⊥BC.
故答案为:=,⊥;
②∵点D是线段BC垂直平分线上的点,
∴BD=DC.
故答案为:线段垂直平分线的性质;
③∵BD=CD,
∴BD+AD=CD+AD=AC,
∴△ABD的周长=AB+AC=3+7=10.
故答案为:10.
∴BE=CE,DE⊥BC.
故答案为:=,⊥;
②∵点D是线段BC垂直平分线上的点,
∴BD=DC.
故答案为:线段垂直平分线的性质;
③∵BD=CD,
∴BD+AD=CD+AD=AC,
∴△ABD的周长=AB+AC=3+7=10.
故答案为:10.
点评:本题考查的是线段垂直平分线的性质,熟知线段垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.

练习册系列答案
相关题目
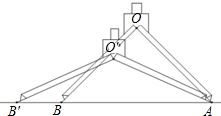 如图,某同学用圆规BOA画一个半径为4cm的圆,测得此时∠O=90°,为了画一个半径更大的同心圆,固定A端不动,将B端向左移至B′处,此时测得∠O′=120°,则BB′的长为( )
如图,某同学用圆规BOA画一个半径为4cm的圆,测得此时∠O=90°,为了画一个半径更大的同心圆,固定A端不动,将B端向左移至B′处,此时测得∠O′=120°,则BB′的长为( )A、2
| ||
B、
| ||
C、2
| ||
D、2-
|
当x<1时,化简
的结果为( )
| (x-1)2 |
| A、x-1 | B、-x-1 |
| C、1-x | D、x+1 |
计算(3m-2n)(-3m-2n)的结果是( )
| A、9m2-4n2 |
| B、9m2+4n2 |
| C、-9m2-4n2 |
| D、-9m2+4n2 |
 如图,在Rt△ABD中,∠D=90°,BP是∠ABD的平分线.
如图,在Rt△ABD中,∠D=90°,BP是∠ABD的平分线. 如图,CF⊥AB,ED⊥AB,垂足分别是F、D,且∠1=∠2.试判断FG与BC的位置关系,并说明理由.
如图,CF⊥AB,ED⊥AB,垂足分别是F、D,且∠1=∠2.试判断FG与BC的位置关系,并说明理由.