题目内容
解下列不等式(组),并把解集在数轴上表示出来:
(1)
x-1>2x;
(2)1+
>5-
.
(1)
| 3 |
| 2 |
(2)1+
| x |
| 3 |
| x-2 |
| 2 |
考点:解一元一次不等式,在数轴上表示不等式的解集
专题:
分析:(1)分别移项、系数化为1求解,然后把解集在数轴上表示出来;
(2)分别去分母、移项、系数化为1求解,然后把解集在数轴上表示出来.
(2)分别去分母、移项、系数化为1求解,然后把解集在数轴上表示出来.
解答:解:(1)移项得:
x<-1,
系数化为1得:x<-2.
在数轴上表示为:
 ;
;
(2)去分母得:6+2x>30-3x+6,
移项得:5x>30,
系数化为1得:x>6,
在数轴上表示为:
 .
.
| 1 |
| 2 |
系数化为1得:x<-2.
在数轴上表示为:
 ;
;(2)去分母得:6+2x>30-3x+6,
移项得:5x>30,
系数化为1得:x>6,
在数轴上表示为:
 .
.点评:本题考查了解一元一次不等式,解不等式要依据不等式的基本性质:
(1)不等式的两边同时加上或减去同一个数或整式不等号的方向不变;
(2)不等式的两边同时乘以或除以同一个正数不等号的方向不变;
(3)不等式的两边同时乘以或除以同一个负数不等号的方向改变.
(1)不等式的两边同时加上或减去同一个数或整式不等号的方向不变;
(2)不等式的两边同时乘以或除以同一个正数不等号的方向不变;
(3)不等式的两边同时乘以或除以同一个负数不等号的方向改变.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
已知圆锥的底面半径为6,侧面积为60π,则这个圆锥的母线为( )
| A、6 | B、8 | C、10 | D、12 |
下列各式中,可用平方差公式分解因式的是( )
| A、a2+b2 |
| B、-a2-b2 |
| C、-a2+b2 |
| D、a2+(-b)2 |
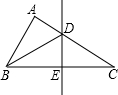 如图,在△ABC中,BC边上的垂直平分线交AC于点D,
如图,在△ABC中,BC边上的垂直平分线交AC于点D, 为了方便学生安全出行,我市推出了学生公交专线.某校对学生出行情况作简要调查后,初步整理了一份信息(如图).根据信息,解答下列问题.
为了方便学生安全出行,我市推出了学生公交专线.某校对学生出行情况作简要调查后,初步整理了一份信息(如图).根据信息,解答下列问题.