题目内容
13.如图,在平面直角坐标系xOy中,AB⊥x轴于点B,AB=3,OB=4,将△OAB绕着原点O逆时针旋转90°,得到△OA1B1;再将△OA1B1绕着线段OB1的中点旋转180°,得到△OA2B1,抛物线y=ax2+bx+c(a≠0)经过点B、B1、A2.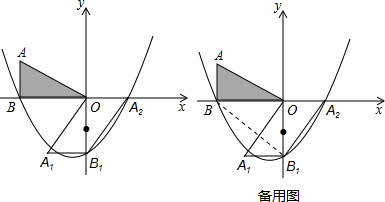
(1)求抛物线的解析式.
(2)在第三象限内,抛物线上的点P在什么位置时,△PBB1的面积最大?求出这时点P的坐标.
(3)在第三象限内,抛物线上是否存在点Q,使点Q到线段BB1的距离为$\frac{\sqrt{2}}{2}$?若存在,求出点Q的坐标;若不存在,请说明理由.
分析 (1)先求出点B、B1、A2的坐标,再用待定系数法求解即可;
(2)设出P点的横坐标,其纵坐标用横坐标表示,求出直线BB1的解析式,过点P作y轴的平行线交BB1于点C,用P点的横坐标表示出线段PC的长度即可用铅垂高法表示出△PBB1的面积,最后利用配方法求最大值;
(3)求出BB1的长度,由于告诉了点Q到线段BB1的距离为$\frac{\sqrt{2}}{2}$,故可求出三角形QBB1的面积,过点Q作y轴的平行线交BB1于点D,设出Q点的坐标,用(2)中所用方法表示出三角形QBB1的面积,建立方程,解之即可.
解答 解:(1)根据旋转的性质可知:△ABO≌A1B1O≌A2B1O,
∵AB=3,OB=4,
∴A(-4,3),B(-4,0),A1(-3,-4),B1(0,-4),A2(3,0),
设抛物线的解析式为y=ax2+bx+c,
将B(-4,0),B1(0,-4),A2(3,0)代入y=ax2+bx+c可得:
$\left\{\begin{array}{l}{16a-4b+c=0}\\{c=-4}\\{9a+3b+c=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{1}{3}}\\{b=\frac{1}{3}}\\{c=-4}\end{array}\right.$,
∴抛物线的解析式为:$y=\frac{1}{3}{x}^{2}+\frac{1}{3}x-4$;
(2)如图1,过点P作PC∥y轴交BB1于点C,
∵B(-4,0),B1(0,-4),
∴直线BB1的解析式为:y=-x-4,
设P(m,$\frac{1}{3}{m}^{2}+\frac{1}{3}m-4$),则C(m,-m-4),
∴${S}_{△P{B}_{1}B}=\frac{1}{2}×({x}_{{B}_{1}}-{x}_{B})×({y}_{C}-{y}_{P})$=$\frac{1}{2}×4×(-m-4-\frac{1}{3}{m}^{2}-\frac{1}{3}m+4)$=$-\frac{2}{3}(m+2)^{2}+\frac{8}{3}$,
∴当m=-2时,△PBB1的面积最大,
此时,P点的坐标为(-2,$-\frac{10}{3}$);
(3)如图2,过点Q作QD∥y轴交BB1于点D,
设Q(n,$\frac{1}{3}{n}^{2}+\frac{1}{3}n-4$),则D(n,-n-4),
∵B(-4,0),B1(0,-4),
∴$B{B}_{1}=4\sqrt{2}$,
∵点Q到线段BB1的距离为$\frac{\sqrt{2}}{2}$,
∴${S}_{△QB{B}_{1}}$=$\frac{1}{2}×4\sqrt{2}×\frac{\sqrt{2}}{2}$=2,
∵${S}_{△QB{B}_{1}}=\frac{1}{2}×({x}_{{B}_{1}}-{x}_{B})×({y}_{D}-{y}_{Q})$=$\frac{1}{2}×4×(-n-4-\frac{1}{3}{n}^{2}-\frac{1}{3}n+4)$=$-\frac{2}{3}{n}^{2}-\frac{4}{3}n$,
∴$-\frac{2}{3}{n}^{2}-\frac{4}{3}n=2$,
解得:n=-3或n=1(舍去),
此时Q点的坐标为(-3,-2);
点评 本题考查了旋转的性质、待定系数法求二次函数解析式、三角形面积的坐标表示、配方法求二次函数最值,等积变换等多个知识点,有一定综合性,难度适中.第(2)问和第(3)问本质上是一样的,关键是用动点的横坐标将三角形面积表示出来.

| A. | 5 | B. | -3 | C. | 5或-3 | D. | 以上都不对 |
 用尺规作图的方法在△ABC中分别画出:
用尺规作图的方法在△ABC中分别画出: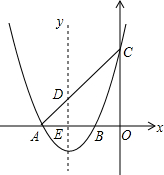 如图,抛物线y=x2+4x+3交x轴于A、B两点,(A在B左侧),交y轴于点C.
如图,抛物线y=x2+4x+3交x轴于A、B两点,(A在B左侧),交y轴于点C.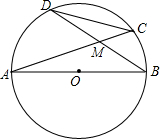 如图,AB为圆O的直径,C,D为圆上两点,$\widehat{CD}$=$\widehat{AD}$+$\widehat{BC}$,连AC、BD相交于M,AB=4,CM=$\sqrt{2}$,求AM的长.
如图,AB为圆O的直径,C,D为圆上两点,$\widehat{CD}$=$\widehat{AD}$+$\widehat{BC}$,连AC、BD相交于M,AB=4,CM=$\sqrt{2}$,求AM的长.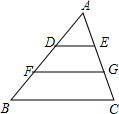 如图,△ABC中,D、F是边AB的三等分点,E、G是边AC的三等分点,如果DE=3cm,那么BC=9cm.
如图,△ABC中,D、F是边AB的三等分点,E、G是边AC的三等分点,如果DE=3cm,那么BC=9cm. 如图,四边形ABCD沿直线AC对折后重合,若AD=3,BC=2,则四边形ABCD周长为10.
如图,四边形ABCD沿直线AC对折后重合,若AD=3,BC=2,则四边形ABCD周长为10.