题目内容

8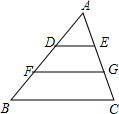．如图，△ABC中，D、F是边AB的三等分点，E、G是边AC的三等分点，如果DE=3cm，那么BC=9cm．

分析 根据D、F是边AB的三等分点，E、G是边AC的三等分点，于是得到$\frac{AD}{AB}=\frac{AE}{AC}$=$\frac{1}{3}$，推出△ADE∽△ABC，根据相似三角形的性质即可得到结论．

解答 解：∵D、F是边AB的三等分点，E、G是边AC的三等分点，
∴$\frac{AD}{AB}=\frac{AE}{AC}$=$\frac{1}{3}$，
∵∠A=∠A，
∴△ADE∽△ABC，
∴$\frac{DE}{BC}=\frac{AD}{AB}$=$\frac{1}{3}$，
∵DE=3cm，
∴BC=9cm，
故答案为：9．

点评 本题考查了相似三角形的判定和性质，熟练掌握相似三角形的判定和性质是解题的关键．

练习册系列答案
相关题目
17．x表示一个一位数，y表示一个两位数，如果将x放在y的左边，则得到一个三位（　　）
A．x+yB．10x+yC．10y+xD．100x+y
18．某学校计划购买若干台电脑，现从两家商场了解到同一型号的电脑每台报价均为6000元，并且多买都有一定的优惠．甲商场的优惠条件是：第一台按原价收款，其余每台优惠25%；乙商场的优惠条件是：每台优惠20%．
（1）若购买4台，哪家商场较优惠？买6台呢？
（2）买多少台，两家商场收费一样多？
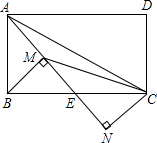16．在矩形ABCD中，AD=$\sqrt{2}$AB，E为BC边的中点，过B、C两点分别作AE的垂线，M、N为垂足，连接CM、AC，则下列结论：
（1）M为AN的中点；（2）CM=CD；（3）△MCN∽△ACD；（4）∠BCM=∠CAN．
其中正确结论的是（1）（2）（3）（4）．并证明你的结论．
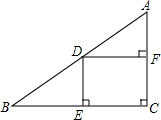3．如图，△ABC中，∠C=90°，D是AB上一点，过点D作DE⊥BC于E，DF⊥AC于F，AC=6，BC=8．
（1）求证：四边形DECF是矩形；
（2）设AD=x，试用含x的式子分别表示DE和DF；
（3）在（2）的条件下，能否使四边形DECF的面积是△ABC面积的一半？如果能，试说明点D在什么位置上；如果不能，试说明理由．
13．如图，在平面直角坐标系xOy中，AB⊥x轴于点B，AB=3，OB=4，将△OAB绕着原点O逆时针旋转90°，得到△OA1B1；再将△OA1B1绕着线段OB1的中点旋转180°，得到△OA2B1，抛物线y=ax2+bx+c（a≠0）经过点B、B1、A2．

（1）求抛物线的解析式．
（2）在第三象限内，抛物线上的点P在什么位置时，△PBB1的面积最大？求出这时点P的坐标．
（3）在第三象限内，抛物线上是否存在点Q，使点Q到线段BB1的距离为$\frac{\sqrt{2}}{2}$？若存在，求出点Q的坐标；若不存在，请说明理由．
20．阅读材料：
已知方程x2+x-1=0，求一个一元二次方程，使它的根分别是已知方程根的2倍．
解：设所求方程的根为y，则y=2x，所以$x=\frac{y}{2}$，
把x=$\frac{y}{2}$带入已知方程，得（$\frac{y}{2}$）2+$\frac{y}{2}-1=0$，
化简得y2+2y-4=0，
所以，所求方程为y2+2y-4=0，
这种利用方程根的代换求新方程的方法叫做“换根法”．
利用阅读材料提供的换根法求新方程：
（1）已知方程x2+x-2=0，求一个一元二次方程，使它的根分别是已知方程根的相反数，则所求方程为y2-y-2=0．
（2）已知方程x2+3x-5=0，求一个一元二次方程，使它的根分别比已知方程的根大1，则所求方程为y2+y-7=0．
17．如果|m-1|=5，则m=6或-4．
18．若a、b是非零实数，则下列说法正确的是（　　）
A．若a2＞a，则a＞1B．若a2＞a，则a2b＞ab
C．若a2＞a，则a2-b2＞a-b2D．若a2＞a，则-a2b＜-ab

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网