题目内容
 如图,正方形ABCD的边长为2,M是BC的中点,将正方形折叠,使点A和点M重合,折痕为EF,求EF和AE的长.
如图,正方形ABCD的边长为2,M是BC的中点,将正方形折叠,使点A和点M重合,折痕为EF,求EF和AE的长.考点:翻折变换(折叠问题)
专题:
分析:在Rt△ABM中,利用勾股定理,求出AM的长度;通过AA证明△EAG∽△MAB,根据相似三角形的性质可得AE的长;过F作FH⊥AB,垂足为H,证明△FHE≌△ABM,根据全等三角形的性质即可求解.
解答:解:在Rt△ABM中,AB=2,BM=
BC=1,
由勾股定理得AM=
=
,
由折叠的性质可知AN=
AM=
,AM⊥EF,
∴∠AGE=90°,
又∵∠EAG=∠MAB,
∴△EAG∽△MAB,
 ∴AE:AM=AG:AB
∴AE:AM=AG:AB
即AE:
=
:2,
解得AE=
,
过F作FH⊥AB,垂足为H,
在△FHE与△ABM中,
,
∴△FHE≌△ABM(AAS),
∴EF=AM=
.
| 1 |
| 2 |
由勾股定理得AM=
| 22+12 |
| 5 |
由折叠的性质可知AN=
| 1 |
| 2 |
| ||
| 2 |
∴∠AGE=90°,
又∵∠EAG=∠MAB,
∴△EAG∽△MAB,
 ∴AE:AM=AG:AB
∴AE:AM=AG:AB即AE:
| 5 |
| ||
| 2 |
解得AE=
| 5 |
| 4 |
过F作FH⊥AB,垂足为H,
在△FHE与△ABM中,
|
∴△FHE≌△ABM(AAS),
∴EF=AM=
| 5 |
点评:考查了翻折问题,翻折问题关键是找准对应重合的量,哪些边、角是相等的.本题中利用相似三角形的判定和性质、勾股定理、全等三角形的知识就迎刃而解.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
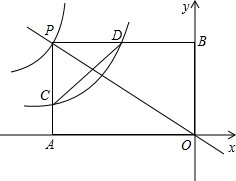 如图,经过原点的直线交双曲线y=-
如图,经过原点的直线交双曲线y=- 如图,飞机于空中A处探测到地面目标C,此时飞行高度AC=1300米,从飞机上看地平面控制点B的俯角α=17°,求飞机A到控制点B的距离.(精确到0.1米:参考数据sin17°=0.29,cos17°=0.96,tan17°=0.31,cot17°=3.30)
如图,飞机于空中A处探测到地面目标C,此时飞行高度AC=1300米,从飞机上看地平面控制点B的俯角α=17°,求飞机A到控制点B的距离.(精确到0.1米:参考数据sin17°=0.29,cos17°=0.96,tan17°=0.31,cot17°=3.30)