题目内容

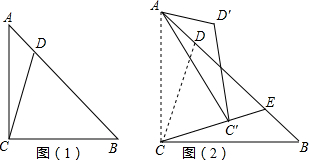
18．如图，在△ABC中，∠C=∠ABC=2∠A．
（1）求∠A的度数；
（2）若AB的垂直平分线MN交AC于D，连BD，求∠DBC的度数．

分析 （1）设∠A=x，由三角形内角和定理列出方程，解方程即可；
（2）根据线段垂直平分线的性质、等腰三角形的性质计算即可．

解答 解：（1）设∠A=x，则∠C=∠ABC=2x，
由三角形内角和定理得，2x+2x+x=180°
∴x=36°，
即∠A的度数为36°；
（2）∵MN垂直平分AB，
∴AD=BD，
∴∠A=∠ABD=36°，
故∠DBC=72°-36°=36°．

点评 本题考查的是线段垂直平分线的性质、等腰三角形的性质，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．

练习册系列答案
相关题目
8．计算：3x2-3（$\frac{1}{3}$x2-2x+1）+4．
9．已知点A在数轴上对应的数为a，点B对应的数为b，且|a+4|+（b-3）2=0．

（1）则a=-4，b=3；并将这两个数在数轴上所对应的点A，B表示出来；
（2）数轴上在B点右边有一点C到A、B两点的距离和为11，若点C的数轴上所对应的数为x，求x的值；
（3）若点A，点B同时沿数轴向正方向运动，点A运动的速度为2单位/秒，点B运动的速度为1单位/秒，若|AB|=4，求运动时间t的值．
（温馨提示：M、N之间距离记作|MN|，点M、N在数轴上对应的数分别为m、n，则|MN|=|m-n|．）
6．计算：
（1）（-3）×2-20÷（-4）+（-12）÷3
（2）已知|x-3|+（y+$\frac{1}{2}$）2=0，求xy的值．
13．用小正方体搭一个几何体，使得从上面和正面看它的图形如图所示．
（1）这个几何体最少需要多少个正方体？最多需要多少个正方体？
（2）画出最少和最多正方体组成几何体时，从左面看的图形（注意：每种情况都要画出）
3．解答下列问题：
（1）已知一元二次方程ax2+bx+c=0（a≠0）有两根x1，x2（b2-4ac≥0）．用求根公式写出x1，x2，并证明x1+x2=-$\frac{b}{a}$，x1x 2=$\frac{c}{a}$
（2）若一元二次方程x2+x-1=0的两根为m，n，运用（1）中的结论，求$\frac{n}{m}$+$\frac{m}{n}$的值．
10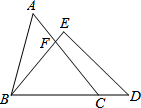．如图，在△ABC和△BDE中，点C在边BD上，边AC交边BE于点F．若AC=BD，AB=ED，BC=BE，则∠ACB等于（　　）
A．∠EDBB．∠BEDC．2∠ABFD．$\frac{1}{2}$∠AFB
7．当x=-2时，求2（4x+x2）-（x2+3x）的值．
8．如图（1），在Rt△ABC中，∠ACB=90°，AC=BC，点D为AB边上一点，连接CD，∠ADC=120°，把△ADC绕点A逆时针旋转30°得△AD′C′，如图（2），连接CC′并延长，交AB于点E．
（1）发现：在图（1）中，∠DCB的度数为75°；在图（2）中，∠DEC′的度数为60°．
（2）论证：在图（2）中，线段D′C′与线段CE有怎样的位置关系和数量关系？并说明理由．
（3）应用：若△ADC绕点A逆时针旋转的度数为m（0°≤m≤360°），以A、B、C、C′四点组成的四边形能否为平行四边形？若能，请直接写出m的值；若不能，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网