题目内容
8. 如图,在△ABC中,∠C=90,∠CAB=60°,按以下步骤作图:①分别以A、B为圆心,以大于$\frac{1}{2}AB$的长为半径作弧,两弧相交于点P和Q;②作直线PQ交AB于点D,交BC于点E.若BE=6,则线段CE的长为3.
如图,在△ABC中,∠C=90,∠CAB=60°,按以下步骤作图:①分别以A、B为圆心,以大于$\frac{1}{2}AB$的长为半径作弧,两弧相交于点P和Q;②作直线PQ交AB于点D,交BC于点E.若BE=6,则线段CE的长为3.
分析 连结AE,如图,利用互余可计算出∠B=30°,再由作法得PQ垂直平分AB,根据线段垂直平分线的性质得EA=EB=6,所以∠EAB=∠B=30°,则∠CAE=30°,然后根据含30度的直角三角形三边的关系得到CE=3.
解答 解:连结AE,如图,
∵∠C=90,∠CAB=60°,
∴∠B=30°,
由作法得PQ垂直平分AB,则EA=EB=6,
∴∠EAB=∠B=30°,
∴∠CAE=30°,
∴CE=$\frac{1}{2}$AE=$\frac{1}{2}$×6=3.
故答案为3.
点评 本题考查了基本作图:掌握基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线).也考查了线段垂直平分线的性质.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
3.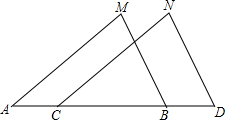 如图,已知MB=ND,MB∥ND,添加下列条件后,仍不能判定△ABM≌△CDN的是( )
如图,已知MB=ND,MB∥ND,添加下列条件后,仍不能判定△ABM≌△CDN的是( )
 如图,已知MB=ND,MB∥ND,添加下列条件后,仍不能判定△ABM≌△CDN的是( )
如图,已知MB=ND,MB∥ND,添加下列条件后,仍不能判定△ABM≌△CDN的是( )| A. | AM=CN | B. | AC=BD | C. | ∠M=∠N | D. | AM∥CN |
 如图,D是△ABC的外角平分线与BA延长线的交点,试判断∠BAC与∠B的大小关系,并说明理由.
如图,D是△ABC的外角平分线与BA延长线的交点,试判断∠BAC与∠B的大小关系,并说明理由.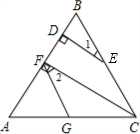 请将下列证明过程中的理由或步骤补充完整:
请将下列证明过程中的理由或步骤补充完整: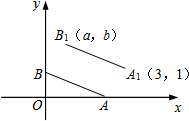 如图,A,B的坐标为(2,0),(0,1),若将线段AB平移至A1B1,则a+b的值为( )
如图,A,B的坐标为(2,0),(0,1),若将线段AB平移至A1B1,则a+b的值为( )