题目内容
13．
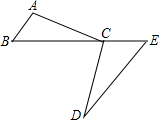已知：如图，C为BE上一点，点A，D分别在BE两侧．AB∥ED，AB=CE，BC=ED．求证：∠A=∠DCE．
分析 根据AB∥ED推出∠B=∠E，再利用SAS判定△ABC≌△CED从而得出结论
解答 证明：∵AB∥ED，
∴∠B=∠E，
在△ABC和△CED中，
$\left\{\begin{array}{l}{AB=CE}\\{∠B=∠E}\\{BC=ED}\end{array}\right.$，
∴△ABC≌△CED，
∴∠A=∠DCE．
点评 本题主要考查了平行线的性质，全等三角形的判定与性质，是一道很简单的全等证明，只需证一次全等，无需添加辅助线，且全等的条件都很明显，关键是熟记全等三角形的判定与性质．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
3．若（ ）÷$\frac{2}{3}$xn=$\frac{1}{2}$xn-2xm+1，则括号内应填的代数式为（ ）
| A． | $\frac{1}{3}$x${\;}^{{n}^{2}}$-2xnm+1 | B． | $\frac{1}{3}$x${\;}^{{n}^{2}}$-$\frac{1}{3}$xnm+$\frac{2}{3}$xn | ||
| C． | $\frac{1}{3}$x2n-$\frac{4}{3}$xm+n+$\frac{2}{3}$xn | D． | $\frac{1}{3}$x2n-$\frac{4}{3}$xm+n+1 |
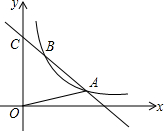如图：一次函数的图象与y轴交于C（0，4），且与反比例函数y=$\frac{k}{x}$（x＞0）的图象在第一象限内交于A（3．a），B（1，b）两点．
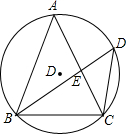如图，AB=AC，弦BD⊥AC于点E．
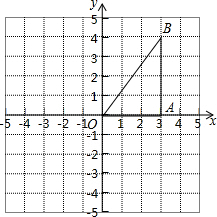在10×10的网格纸上建立平面直角坐标系如图所示，在直角三角形ABO中，∠OAB=90°，且点B的坐标为（3，4）．