题目内容
8.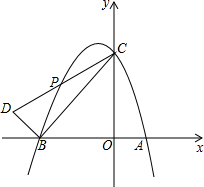 如图,抛物线y=-$\frac{1}{2}$x2+bx+4与x轴交于A(2,0)、B两点,与y轴交于点C.
如图,抛物线y=-$\frac{1}{2}$x2+bx+4与x轴交于A(2,0)、B两点,与y轴交于点C.(1)求b的值;
(2)求抛物线的对称轴及顶点坐标;
(3)以点B为直角顶点,BC为直角边作Rt△BCD,CD交抛物线于第二象限的点P,若PC=PD,求P点的坐标.
分析 (1)将A点坐标代入即可求出;
(2)直接用对称轴公式与顶点坐示公式计算即可;
(3)连接BP,则BP直角角三角形斜边CD上的中线,即BP=CP,连接OP,可证△BPO与△CPO全等,从而OP平分∠BOC,设出P点坐标代入抛物线解析式即可解出.
解答 解:(1)将A(2,0)代入y=-$\frac{1}{2}$x2+bx+4得b=-1.
(2)对称轴$-\frac{b}{2a}=-\frac{-1}{2×(-\frac{1}{2})}=-1$.
$\frac{4ac-{b}^{2}}{4a}=4-\frac{(-1)^{2}}{4×(-\frac{1}{2})}=\frac{9}{2}$,
∴顶点坐标:(-1,$\frac{9}{2}$).
(3)连接PB,PO,如图,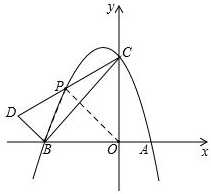
令$-\frac{1}{2}{x}^{2}-x+4=0$,解得x1=-4,x2=2,
∴B(-4,0),
当x=0时,y=4,
∴C(0,4),
∴OB=OC,
在Rt△BDC中,∵PC=PD,
∴BP=PC,
在△BPO和△CPO中,
$\left\{\begin{array}{l}{BP=PC}\\{PO=PO}\\{CO=BO}\end{array}\right.$,
∴△BPO≌△CPO(SSS),
∴OP平分∠COB,
设P(m,-m),
则有$-\frac{1}{2}{a}^{2}-a+4=-a$,解得:m=$±2\sqrt{2}$,
又P在第二象限,
∴P($-2\sqrt{2}$,$2\sqrt{2}$).
点评 本题考查了待定系数法求二次函数解析式、抛物线的对称轴公式与顶点坐标公式、直角三角形斜中线定理、全等三角形的判定与性质、解一元二次方程等多个知识点,有一定综合性,难度适中.第(3)问当中,证明△BPO≌△CPO是关键.

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案| A. | $\frac{1}{3}$ | B. | 3 | C. | -$\frac{1}{3}$ | D. | -3 |
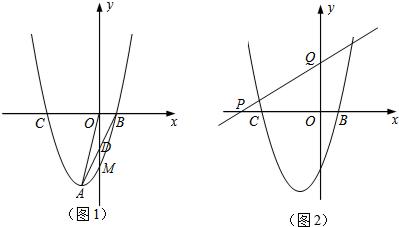
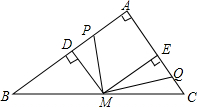 如图所示,P、Q分别是Rt△ABC两直角边AB、AC上两点,M为斜边BC的中点,且PM⊥QM,MD⊥AB于点D,ME⊥AC于点E.求证:
如图所示,P、Q分别是Rt△ABC两直角边AB、AC上两点,M为斜边BC的中点,且PM⊥QM,MD⊥AB于点D,ME⊥AC于点E.求证: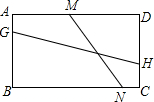 如图,已知矩形ABCD,AD=9,AB=6,若点G、H、M、N分别在AB、CD、AD、BC上,线段MN与GH交于点K.若∠GKM=45°,NM=3$\sqrt{5}$,则GH=3$\sqrt{10}$.
如图,已知矩形ABCD,AD=9,AB=6,若点G、H、M、N分别在AB、CD、AD、BC上,线段MN与GH交于点K.若∠GKM=45°,NM=3$\sqrt{5}$,则GH=3$\sqrt{10}$.