题目内容
14.(1)若单项式3ab2n-1与-4ab5-n的和仍是单项式,则n的值为2(2)若a、b互为相反数,c、d互为倒数,p的绝对值等于1,则关于x的方程(a+b)x2+3cd•x-p2=0的解为x=$\frac{1}{3}$.
分析 (1)根据题意得到两单项式为同类项,求出n的值即可;
(2)利用相反数,倒数,以及绝对值的代数意义求出a+b,cd,p的值,代入方程即可求出解.
解答 解:(1)∵单项式3ab2n-1与-4ab5-n的和仍是单项式,
∴2n-1=5-n,
解得:n=2;
(2)由题意得:a+b=0,cd=1,p=1或-1,
代入方程得:3x-1=0,
解得:x=$\frac{1}{3}$,
故答案为:(1)2;(2)x=$\frac{1}{3}$
点评 此题考查了解一元一次方程,相反数,绝对值,以及倒数,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
19.下列方程组中,是三元一次方程组的是( )
| A. | $\left\{\begin{array}{l}{a=1}\\{b=2}\\{b-c=3}\\{\;}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=2}\\{y+z=1}\\{z+c=3}\\{\;}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{4x-3y=7}\\{5x-2y=14}\\{2x-y=4}\\{\;}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{xy+z=3}\\{x+yz=5}\\{xy+y=7}\\{\;}\end{array}\right.$ |
 如图,在四边形ABCD中,E、F分别在BC、AD上,且AF=CE,连接EF,与对角线BD交于点O.若EF、BD互相平分,试判断四边形ABCD的形状,并说明理由.
如图,在四边形ABCD中,E、F分别在BC、AD上,且AF=CE,连接EF,与对角线BD交于点O.若EF、BD互相平分,试判断四边形ABCD的形状,并说明理由.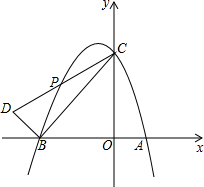 如图,抛物线y=-$\frac{1}{2}$x2+bx+4与x轴交于A(2,0)、B两点,与y轴交于点C.
如图,抛物线y=-$\frac{1}{2}$x2+bx+4与x轴交于A(2,0)、B两点,与y轴交于点C.