题目内容
9. 如图所示,化简:$\sqrt{(a-b)^{2}}$-$\sqrt{{a}^{2}}$=b.
如图所示,化简:$\sqrt{(a-b)^{2}}$-$\sqrt{{a}^{2}}$=b.
分析 由数轴可得:a<0<b,则a-b<0,再根据二次根式的性质,进行化简,即可解答.
解答 解:由数轴可得:a<0<b,
则a-b<0,
$\sqrt{(a-b)^{2}}-\sqrt{{a}^{2}}$
=b-a+a
=b.
故答案为:b.
点评 本题考查了二次根式的化简,解决本题的关键是由数轴确定a,b的正负.

练习册系列答案
相关题目
17.若a2-2a+1+|b-2|=0,则以a、b为边长的等腰三角形的周长为( )
| A. | 4 | B. | 5 | C. | 4或5 | D. | 无法确定 |
1.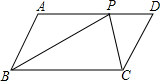 如图,平行四边形ABCD中,P是边AD上间任意一点(除点A,D外),△ABP,△BCP,△CDP的面积分别为S1,S2,S3,则一定成立的是( )
如图,平行四边形ABCD中,P是边AD上间任意一点(除点A,D外),△ABP,△BCP,△CDP的面积分别为S1,S2,S3,则一定成立的是( )
 如图,平行四边形ABCD中,P是边AD上间任意一点(除点A,D外),△ABP,△BCP,△CDP的面积分别为S1,S2,S3,则一定成立的是( )
如图,平行四边形ABCD中,P是边AD上间任意一点(除点A,D外),△ABP,△BCP,△CDP的面积分别为S1,S2,S3,则一定成立的是( )| A. | S1+S3<S2 | B. | S1+S3>S2 | C. | S1+S3=S2 | D. | S1+S2=S3 |
19.若|x+y-1|+(y+3)2=0,则$\frac{1}{4}$x-2y的值是( )
| A. | 1 | B. | -1 | C. | 7 | D. | -7 |
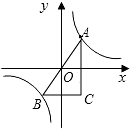 如图,点A(2,y)是反比例函数y=$\frac{12}{x}$的图象上一点,延长AO交该图象于点B,AC⊥x轴,BC⊥y轴,求△ABC的面积.
如图,点A(2,y)是反比例函数y=$\frac{12}{x}$的图象上一点,延长AO交该图象于点B,AC⊥x轴,BC⊥y轴,求△ABC的面积. 实数a、b、c在数轴上的位置如图所示,化简:$\sqrt{(a-b)^{2}}$-|a+c|+$\sqrt{(c-b)^{2}}$-|-2b|.
实数a、b、c在数轴上的位置如图所示,化简:$\sqrt{(a-b)^{2}}$-|a+c|+$\sqrt{(c-b)^{2}}$-|-2b|.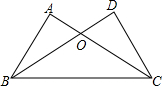 如图,AC、BD相交于点O,∠A=∠D,请你根据(SAS)全等三角形的判定再补充一个条件,使得△ABC≌△DCB,你补充的条件是OB=OC.
如图,AC、BD相交于点O,∠A=∠D,请你根据(SAS)全等三角形的判定再补充一个条件,使得△ABC≌△DCB,你补充的条件是OB=OC.