题目内容
12.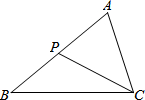 如图,点P为△ABC的AB边上一点(AB>AC),下列条件中不一定能保证△ACP∽△ABC的是( )
如图,点P为△ABC的AB边上一点(AB>AC),下列条件中不一定能保证△ACP∽△ABC的是( )| A. | ∠ACP=∠B | B. | ∠APC=∠ACB | C. | $\frac{PC}{BC}$=$\frac{AC}{AB}$ | D. | $\frac{AC}{AB}$=$\frac{AP}{AC}$ |
分析 根据相似三角形的判定方法.利用公共角∠A进行求解.
解答 解:∵∠A=∠A,
∴当∠APC=∠ACB或∠ACP=∠B或AC:AB=AP:AC或AC2=AB•AP时,
△ACP∽△ABC.
故选C.
点评 此题考查了相似三角形的判定:①有两个对应角相等的三角形相似;②有两个对应边的比相等,且其夹角相等,则两个三角形相似;③三组对应边的比相等,则两个三角形相似,熟记相似三角形的各种判定方法是解题关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
20.点P(-5,5)在平面直角坐标系中所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
1. 在△ABC中,D是BC上的一点,且△ABD与△ADC的面积相等,则线段AD为△ABC的( )
在△ABC中,D是BC上的一点,且△ABD与△ADC的面积相等,则线段AD为△ABC的( )
 在△ABC中,D是BC上的一点,且△ABD与△ADC的面积相等,则线段AD为△ABC的( )
在△ABC中,D是BC上的一点,且△ABD与△ADC的面积相等,则线段AD为△ABC的( )| A. | 高 | B. | 角平分线 | C. | 中线 | D. | 不能确定 |
 已知:如图所示的网格中有△ABC,
已知:如图所示的网格中有△ABC, 如图,点A、B、C是⊙O上的三点,AB∥OC.
如图,点A、B、C是⊙O上的三点,AB∥OC.