题目内容
7.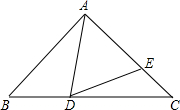 如图,在△ABC中,∠BAC=90°,AB=AC,点D、E分别在BC、AC上,且∠ADE=45°.
如图,在△ABC中,∠BAC=90°,AB=AC,点D、E分别在BC、AC上,且∠ADE=45°.(1)求证:△ABD∽△DCE;
(2)若AB=2,BD=1,求CE的长.
分析 (1)要证△ABD∽△DCE,根据已知,可知∠B=∠C,只需要再证∠DEC=∠ADB,利用三角形的外角等于不相邻的两内角之和,可证.那么△ABD∽△DCE;
(2)由AB=2,可得到BC=2$\sqrt{2}$,由(1)知△ABD∽△DCE,根据相似三角形的性质即可得到结论.
解答 解:(1)∵∠BAC=90°,AB=AC,
∴∠B=∠C=45°,
又因为∠DEC=∠ADE+∠CAD=45°+∠CAD(三角形的外角等于不相邻的两个内角之和),
同理∠ADB=∠C+∠CAD=45°+∠CAD,
∴∠DEC=∠ADB,
又∠ABD=∠DCE=45°,
∴△ABD∽△DCE;
(2)∵AB=2,
∴BC=2$\sqrt{2}$,
∵△ABD∽△DCE,
∴$\frac{AC}{BD}=\frac{CD}{AE}$,
∴$\frac{2}{1}=\frac{2\sqrt{2}-1}{AE}$,
∴AE=$\frac{2\sqrt{2}-1}{2}$.
点评 本题利用了三角形的外角等于不相邻的两个内角之和,相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解决问题的关键.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
18.某树苗培育基地培育了1000棵银杏树苗,为了解树苗的长势,测量了6棵树苗的高(单位:cm),其分别为51,48,51,49,52,49,则这1000棵树苗的方差的估计值为( )
| A. | 1 | B. | 1.5 | C. | 2 | D. | 3 |
19.下列方程中解为x=2的是( )
| A. | 3x+(10-x)=20 | B. | 4(x+0.5)+x=7 | C. | x=-$\frac{1}{2}$x+3 | D. | $\frac{1}{7}$(x+14)=$\frac{1}{4}$(x+20) |
16.如果a的倒数是-1,那么a2等于( )
| A. | 1 | B. | -1 | C. | 3 | D. | -3 |
17.已知x<1,那么化简$\sqrt{{x^2}-2x+1}$的结果是( )
| A. | x-1 | B. | 1-x | C. | -x-1 | D. | x+1 |
 如图,图4×4正方形网格,每个小正方形的边长为1,请按要求画出下列图形.所画图形的各个顶点均在所给小正方形的顶点上.
如图,图4×4正方形网格,每个小正方形的边长为1,请按要求画出下列图形.所画图形的各个顶点均在所给小正方形的顶点上. 如图,小明用长为3m的竹竿CD做测量共计,测量学校旗杆AB的高度,移动竹竿,使O、C、A在同一直线上,此时OD=6m,DB=12m,则旗杆AB的高为9m.
如图,小明用长为3m的竹竿CD做测量共计,测量学校旗杆AB的高度,移动竹竿,使O、C、A在同一直线上,此时OD=6m,DB=12m,则旗杆AB的高为9m.