题目内容
17. 如图,图4×4正方形网格,每个小正方形的边长为1,请按要求画出下列图形.所画图形的各个顶点均在所给小正方形的顶点上.
如图,图4×4正方形网格,每个小正方形的边长为1,请按要求画出下列图形.所画图形的各个顶点均在所给小正方形的顶点上.(1)在图中画出一个等腰△ABC;
(2)以AC为一边作平行四边形ACED;
(3)直接写出等腰△ABC与平行四边形ACED之间重叠部分面积.
分析 (1)根据等腰三角形定义可以解决.
(2)根据平行四边形定义交于解决.
(3)先求出BM:BA,然后利用相似三角形的性质即可解决.
解答 解:(1)图中△ABC就是所画.
(2)图中平行四边形ACED就是所画.
(3)设AB,DE交于点M,作MN⊥AG,MK⊥GE.
在△AGB和△EGD中,
$\left\{\begin{array}{l}{AG=EG}\\{∠AGB=∠EGD}\\{GB=GD}\end{array}\right.$,
∴△AGB≌△EGD,
∴∠GAB=∠GED
在△AMD和△EMB中,
$\left\{\begin{array}{l}{∠DAM=∠BEM}\\{∠AMD=∠EMB}\\{AD=BE}\end{array}\right.$,
∴△AMD≌△EMB,
∴AM=EM,
在RT△AMN和RT△EMK中,
$\left\{\begin{array}{l}{∠MAN=∠MEK}\\{∠ANM=∠MKE}\\{AM=ME}\end{array}\right.$,
∴△AMN≌△EMK,
∴MN=MK,∴∠MGN=∠MGK=45°,
∴∠NGM=∠NMG=∠MGK=∠KMG=45°,
∴MN=NG=KG=KM,设MN=a,
∵MN∥GB,
∴$\frac{MN}{GB}=\frac{AN}{AG}$,
∴$\frac{a}{3}=\frac{4-a}{4}$,
∴a=$\frac{12}{7}$,
∴$\frac{BM}{BA}=\frac{GN}{GA}=\frac{3}{7}$,
∴$\frac{{S}_{△BMH}}{{S}_{△ABC}}=\frac{9}{49}$,
∵S△ABC=16-$\frac{1}{2}$×3×4-$\frac{1}{2}$×3×4-$\frac{1}{2}$×1×1=$\frac{7}{2}$,
∴S△BMH=$\frac{9}{14}$
∴S重叠AMHC=$\frac{7}{2}$-$\frac{9}{14}$=$\frac{20}{7}$.
点评 本题考查等腰三角形的定义、平行四边形的定义、全等三角形的判定和性质、相似三角形的性质和判定,利用相似三角形的面积比等于相似比的平方是解决问题的关键.

| A. | -0.1>-0.001 | B. | -1>0 | C. | $\frac{1}{2}<\frac{1}{3}$ | D. | -5<3 |
 如图,能表示点到直线(或线段)距离的线段有( )
如图,能表示点到直线(或线段)距离的线段有( )| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |


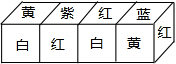 把立方体的六个面分别涂上六种不同的颜色(红、绿、蓝、黄、紫、白),现将大小相同,颜色分布完全一样的四个立方体拼成一个水平放置的长方体,如图所示,那么这个长方体中与蓝色一面相对的颜色是白色.
把立方体的六个面分别涂上六种不同的颜色(红、绿、蓝、黄、紫、白),现将大小相同,颜色分布完全一样的四个立方体拼成一个水平放置的长方体,如图所示,那么这个长方体中与蓝色一面相对的颜色是白色.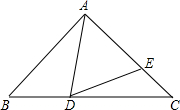 如图,在△ABC中,∠BAC=90°,AB=AC,点D、E分别在BC、AC上,且∠ADE=45°.
如图,在△ABC中,∠BAC=90°,AB=AC,点D、E分别在BC、AC上,且∠ADE=45°.