题目内容
8.已知关于x的方程x2+2x+a-2=0.(1)若该方程有两个不相等的实数根,求实数a的取值范围;
(2)当该方程的一个根为1时,求a的值及方程的另一根.
分析 (1)关于x的方程x2-2x+a-2=0有两个不相等的实数根,即判别式△=b2-4ac>0.即可得到关于a的不等式,从而求得a的范围.
(2)设方程的另一根为x1,根据根与系数的关系列出方程组,求出a的值和方程的另一根.
解答 解:(1)∵b2-4ac=(2)2-4×1×(a-2)=12-4a>0,
解得:a<3.
∴a的取值范围是a<3;
(2)设方程的另一根为x1,由根与系数的关系得:
$\left\{\begin{array}{l}{1{+x}_{1}=-2}\\{1{•x}_{1}=a-2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-1}\\{{x}_{1}=-3}\end{array}\right.$,
则a的值是-1,该方程的另一根为-3.
点评 本题考查了一元二次方程根的判别式,一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18. 某班开展安全知识竞赛活动,班长将所有同学的成绩分成四类,并制作了如下的统计图表:
某班开展安全知识竞赛活动,班长将所有同学的成绩分成四类,并制作了如下的统计图表:
根据图表信息,回答下列问题:
(1)该班共有学生40人;表中a=20;
(2)将丁类的五名学生分别记为A、B、C、D、E,现从中随机挑选两名学生参加学校的决赛,请借助树状图、列表或其他方式求B一定能参加决赛的概率.
 某班开展安全知识竞赛活动,班长将所有同学的成绩分成四类,并制作了如下的统计图表:
某班开展安全知识竞赛活动,班长将所有同学的成绩分成四类,并制作了如下的统计图表:| 类别 | 成绩 | 频数 |
| 甲 | 60≤m<70 | 4 |
| 乙 | 70≤m<80 | a |
| 丙 | 80≤m<90 | 10 |
| 丁 | 90≤m≤100 | 6 |
(1)该班共有学生40人;表中a=20;
(2)将丁类的五名学生分别记为A、B、C、D、E,现从中随机挑选两名学生参加学校的决赛,请借助树状图、列表或其他方式求B一定能参加决赛的概率.
19. 如图,在△ABC中,AB=AC,D为BC中点,∠BAD=35°,则∠C的度数为( )
如图,在△ABC中,AB=AC,D为BC中点,∠BAD=35°,则∠C的度数为( )
 如图,在△ABC中,AB=AC,D为BC中点,∠BAD=35°,则∠C的度数为( )
如图,在△ABC中,AB=AC,D为BC中点,∠BAD=35°,则∠C的度数为( )| A. | 35° | B. | 45° | C. | 55° | D. | 60° |
16.|-2015|等于( )
| A. | 2015 | B. | -2015 | C. | ±2015 | D. | $\frac{1}{2015}$ |
13.若x=3是分式方程$\frac{a-2}{x}$-$\frac{1}{x-2}$=0的根,则a的值是( )
| A. | 5 | B. | -5 | C. | 3 | D. | -3 |
17.分式方程$\frac{2}{x-2}+\frac{3x}{2-x}$=1的解为( )
| A. | 1 | B. | 2 | C. | $\frac{1}{3}$ | D. | 0 |
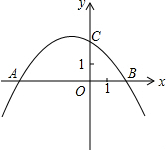 如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A(-4,0),B(2,0),与y轴交于点C(0,2).
如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A(-4,0),B(2,0),与y轴交于点C(0,2).