题目内容
5.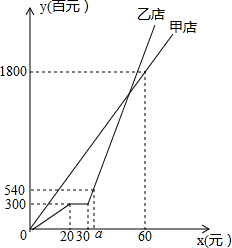 某知名品牌在甲、乙两地的新店同时开张,乙店经营不久为了差异营销而进行了品牌升级,因此停业了一段时间,随后继续营业,第40天结束时两店销售总收入为2100百元.甲、乙两店自开张后各自的销售收入y(百元)随时间x(天)的变化情况如图所示,请根据图象解决下列问题:
某知名品牌在甲、乙两地的新店同时开张,乙店经营不久为了差异营销而进行了品牌升级,因此停业了一段时间,随后继续营业,第40天结束时两店销售总收入为2100百元.甲、乙两店自开张后各自的销售收入y(百元)随时间x(天)的变化情况如图所示,请根据图象解决下列问题:(1)乙店停业了10天;
(2)求出图中a的值;
(3)求出在第几天结束时两店收入相差150百元?
分析 (1)乙店自20天到30天各销售收入没有变化,由此确定乙店停业的天数;
(2)设甲店销售收入y(元)与天数x(天)之间的函数关系式为:y=kx(k≠0),把点(60,1800)代入y=kx+b,求得解析式,然后代入x=40,求得甲店40天的销售收入,从而求得乙店40天的销售收入,然后根据待定系数法求得乙店停业以后的销售收入y(百元)随时间x(天)的函数解析式,把y=540代入即可求得a的值;
(3)先求得停业前,乙店的销售收入y(百元)随时间x(天)的变化的函数解析式为y=15x,然后分三种情况列出方程,解方程即可求得.
解答 解:(1)由图象可知:乙店停业了30-20=10天,
故答案为10;
(2)设甲店销售收入y(元)与天数x(天)之间的函数关系式为:y=kx(k≠0),
把点(60,1800)代入y=kx得:1800=60k,
解得:k=30,
∴y=30x,
把x=40代入得y=40×30=1200,
∴乙店第40天结束时销售收入为2100-1200=900百元,
设乙店停业后销售收入y(元)与天数x(天)之间的函数关系式为:y=mx+n(m≠0),
把点(30,300)和(40,900)代入y=mx+n得:$\left\{\begin{array}{l}{30m+n=300}\\{40m+n=900}\end{array}\right.$
解得:$\left\{\begin{array}{l}{m=60}\\{n=-1500}\end{array}\right.$.
∴y=60x-1500,
把y=540代入得,540=60x-1500,解得x=34,
∴a=34;
(3)由图象可知停业前,乙店的销售收入y(百元)随时间x(天)的变化的函数解析式为y=15x,
根据题意:①30x=15x+150,
解得x=10;
②30x+150=60x-1500,解得x=55,
③30x=60x-1500+150,解得x=45,
所以,当第10天、45天、55天结束时两店收入相差150百元.
点评 本题考查了一次函数的实际应用,解决本题的关键是得到甲店销售收入y(元)与天数x(天)之间的函数关系式,乙店的销售收入y与天数x的函数关系式,进行分类讨论.

 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
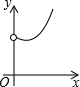
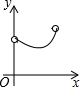
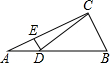 如图,在Rt△ABC中,∠ACB=90°,∠ABC=60°,AB=4,D是AB边上的一个动点(不与点A,B重合),过点D作CD的垂线交射线CA于点E.设AD=x,CE=y,则下列图象中,能表示与的函数关系的图象大致是( )
如图,在Rt△ABC中,∠ACB=90°,∠ABC=60°,AB=4,D是AB边上的一个动点(不与点A,B重合),过点D作CD的垂线交射线CA于点E.设AD=x,CE=y,则下列图象中,能表示与的函数关系的图象大致是( )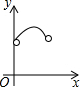

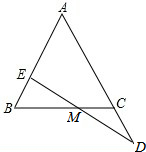 如图,在△ABC中,AB=AC,点E在AB上,点D在AC的延长线上,且BE=CD,ED交BC于点M,求证:EM=DM.
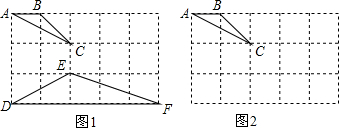
如图,在△ABC中,AB=AC,点E在AB上,点D在AC的延长线上,且BE=CD,ED交BC于点M,求证:EM=DM.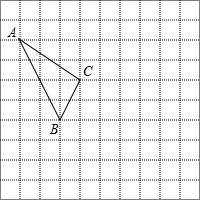 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).
在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).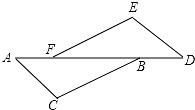 如图,AC∥DE,BC∥EF,AF=DB,求证:△ABC≌△DFE.
如图,AC∥DE,BC∥EF,AF=DB,求证:△ABC≌△DFE.