题目内容
13.如图是3×5的网格,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点,以格点为顶点的三角形叫格点三角形.(1)图1中的格点△ABC与△DEF相似吗?请说明理由;
(2)请在图2中画一个格点△A1B1C1与△ABC相似.(要求:△A1B1C1与△ABC、△DEF都不全等)
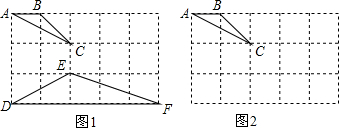
分析 (1)利用勾股定理分别得出三角形各边长,进而利用相似三角形的判定方法得出答案;
(2)利用相似三角形的判定方法,将各边扩大2倍得出答案.
解答 解:(1)△ABC∽△DEF,
理由如下:根据勾股定理可得,
AB=1,BC=$\sqrt{2}$,AC=$\sqrt{5}$,
DE=$\sqrt{5}$,EF=$\sqrt{10}$,DF=5,
∵$\frac{AB}{DE}$=$\frac{1}{\sqrt{5}}$=$\frac{\sqrt{5}}{5}$,$\frac{BC}{EF}$=$\frac{\sqrt{2}}{\sqrt{10}}$=$\frac{\sqrt{5}}{5}$,
$\frac{AC}{DF}$=$\frac{\sqrt{5}}{5}$,
∴$\frac{AB}{DE}$=$\frac{BC}{EF}$=$\frac{AC}{DF}$,
∴△ABC∽△DEF;
(2)如图2所示:△A1B1C1即为所求,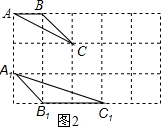 .
.
点评 此题主要考查了相似变换,根据题意得出对应边的长是解题关键.

练习册系列答案
相关题目
3.如果ab>0,则( )
| A. | a>0,b>0 | B. | a<0,b<0 | C. | a、b同号 | D. | a、b异号 |
4.下列各式中是二元一次方程的是( )
| A. | a-πb=9 | B. | xy-y=1 | C. | 5x-y>1 | D. | $\frac{m}{6}+\frac{1}{n}=2$ |
1.如图是一个简单的数值运算程序,当输入的x的值为-1时,则输出的值为( )


| A. | 1 | B. | -5 | C. | -1 | D. | 5 |
18.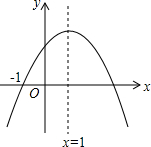 已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论中正确的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论中正确的是( )
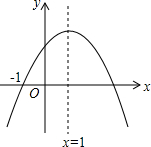 已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论中正确的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论中正确的是( )| A. | ac>0 | B. | 当x>1时,y随x的增大而增大 | ||
| C. | 2a+b=1 | D. | 方程ax2+bx+c=0有一个根是x=3 |
2.下列说法正确的有( )
(1)所有的有理数都能用数轴上的点表示
(2)符号不同的两个数互为相反数
(3)有理数分为正数和负数
(4)两数相减,差一定小于被减数.
(1)所有的有理数都能用数轴上的点表示
(2)符号不同的两个数互为相反数
(3)有理数分为正数和负数
(4)两数相减,差一定小于被减数.
| A. | (1)、(2) | B. | (1)、(3) | C. | (1)、(2)、(3) | D. | (1) |
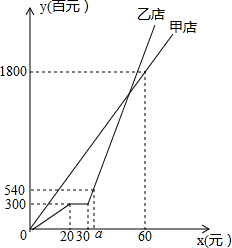 某知名品牌在甲、乙两地的新店同时开张,乙店经营不久为了差异营销而进行了品牌升级,因此停业了一段时间,随后继续营业,第40天结束时两店销售总收入为2100百元.甲、乙两店自开张后各自的销售收入y(百元)随时间x(天)的变化情况如图所示,请根据图象解决下列问题:
某知名品牌在甲、乙两地的新店同时开张,乙店经营不久为了差异营销而进行了品牌升级,因此停业了一段时间,随后继续营业,第40天结束时两店销售总收入为2100百元.甲、乙两店自开张后各自的销售收入y(百元)随时间x(天)的变化情况如图所示,请根据图象解决下列问题: