题目内容
15.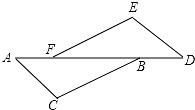 如图,AC∥DE,BC∥EF,AF=DB,求证:△ABC≌△DFE.
如图,AC∥DE,BC∥EF,AF=DB,求证:△ABC≌△DFE.
分析 首先利用平行线的性质可得∠A=∠D,∠CBA=∠EFD,再根据等式的性质可得AB=FD,再利用ASA判定△ABC≌△DFE即可.
解答 证明:∵AC∥DE,
∴∠A=∠D,
∵BC∥EF,
∴∠CBA=∠EFD,
∵AF=DB,
∴AF+FB=DB+FB,
∴AB=FD,
在△ABC和△DFE中$\left\{\begin{array}{l}{∠A=∠D}\\{AB=DF}\\{∠EFD=∠CBA}\end{array}\right.$,
∴△ABC≌△DFE(ASA).
点评 本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
6.某城市大剧院地面的一部分为扇形,观众席的座位按下列方式设置:
按这种方式排下去,
(1)第5、6排各有多少个座位?
(2)第n排有多少个座位?
(3)根据(2)的代数式,判断第25排有多少个座位?
| 排数 | 1 | 2 | 3 | 4 |
| 座位数 | 50 | 53 | 56 | 59 |
(1)第5、6排各有多少个座位?
(2)第n排有多少个座位?
(3)根据(2)的代数式,判断第25排有多少个座位?
10.某校以年级为单位开展广播操比赛,全年级有10个班,每个班有50名学生,规定每班抽25名学生参加比赛,这时样本容量是( )
| A. | 10 | B. | 50 | C. | 500 | D. | 250 |
7.在Rt△ABC中,∠C=90°,若cosA=$\frac{5}{13}$,则sinB的值是( )
| A. | $\frac{5}{13}$ | B. | $\frac{12}{13}$ | C. | $\frac{5}{12}$ | D. | $\frac{12}{5}$ |
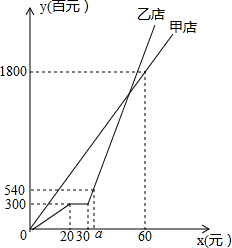 某知名品牌在甲、乙两地的新店同时开张,乙店经营不久为了差异营销而进行了品牌升级,因此停业了一段时间,随后继续营业,第40天结束时两店销售总收入为2100百元.甲、乙两店自开张后各自的销售收入y(百元)随时间x(天)的变化情况如图所示,请根据图象解决下列问题:
某知名品牌在甲、乙两地的新店同时开张,乙店经营不久为了差异营销而进行了品牌升级,因此停业了一段时间,随后继续营业,第40天结束时两店销售总收入为2100百元.甲、乙两店自开张后各自的销售收入y(百元)随时间x(天)的变化情况如图所示,请根据图象解决下列问题: