题目内容
10.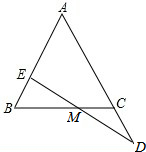 如图,在△ABC中,AB=AC,点E在AB上,点D在AC的延长线上,且BE=CD,ED交BC于点M,求证:EM=DM.
如图,在△ABC中,AB=AC,点E在AB上,点D在AC的延长线上,且BE=CD,ED交BC于点M,求证:EM=DM.
分析 点E作EF∥AC,证得∠EFM=∠DCM,∠FEM=∠D,∠EFB=∠ACB,由AB=AC,得到∠B=∠ACB,证得∠B=∠EFB,得到BE=EF,证得EF=CD,进而证得△EFM和△DCM就可以得出结论.
解答 证明:过点E作EF∥AC交BC于F,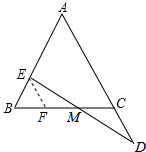
∴∠EFM=∠DCM,∠FEM=∠D,∠EFB=∠ACB,
∵AB=AC,
∴∠B=∠ACB,
∴∠B=∠EFB,
∴BE=EF,
∵BE=CD,
∴EF=CD,
在△EFM和△DCM中,
$\left\{\begin{array}{l}{∠FEM=∠D}\\{EF=CD}\\{∠EFM=∠DCM}\end{array}\right.$,
△EFM和△DCM(ASA),
∴EM=DM.
点评 本题考查了等腰三角形的性质的运用,平行线的性质的运用,全等三角形的判定语言性质的运用,解答时证明三角形全等是关键.

练习册系列答案
相关题目
1.如图是一个简单的数值运算程序,当输入的x的值为-1时,则输出的值为( )


| A. | 1 | B. | -5 | C. | -1 | D. | 5 |
18.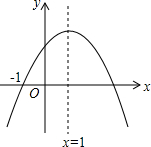 已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论中正确的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论中正确的是( )
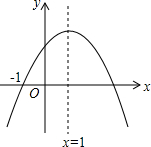 已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论中正确的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论中正确的是( )| A. | ac>0 | B. | 当x>1时,y随x的增大而增大 | ||
| C. | 2a+b=1 | D. | 方程ax2+bx+c=0有一个根是x=3 |
2.下列说法正确的有( )
(1)所有的有理数都能用数轴上的点表示
(2)符号不同的两个数互为相反数
(3)有理数分为正数和负数
(4)两数相减,差一定小于被减数.
(1)所有的有理数都能用数轴上的点表示
(2)符号不同的两个数互为相反数
(3)有理数分为正数和负数
(4)两数相减,差一定小于被减数.
| A. | (1)、(2) | B. | (1)、(3) | C. | (1)、(2)、(3) | D. | (1) |
 已知a、b、c在数轴上位置如图:则代数式|a|+|a+b|+|c-a|-|b-c|的值等于多少?
已知a、b、c在数轴上位置如图:则代数式|a|+|a+b|+|c-a|-|b-c|的值等于多少?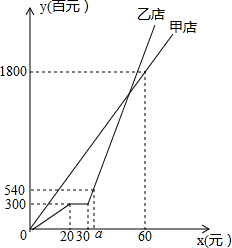 某知名品牌在甲、乙两地的新店同时开张,乙店经营不久为了差异营销而进行了品牌升级,因此停业了一段时间,随后继续营业,第40天结束时两店销售总收入为2100百元.甲、乙两店自开张后各自的销售收入y(百元)随时间x(天)的变化情况如图所示,请根据图象解决下列问题:
某知名品牌在甲、乙两地的新店同时开张,乙店经营不久为了差异营销而进行了品牌升级,因此停业了一段时间,随后继续营业,第40天结束时两店销售总收入为2100百元.甲、乙两店自开张后各自的销售收入y(百元)随时间x(天)的变化情况如图所示,请根据图象解决下列问题: