题目内容
3.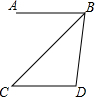 如图,AB∥CD,CB平分∠ABD.若∠C=40°,则∠D的度数为( )
如图,AB∥CD,CB平分∠ABD.若∠C=40°,则∠D的度数为( )| A. | 90° | B. | 100° | C. | 110° | D. | 120° |
分析 先利用平行线的性质易得∠ABC=40°,因为CB平分∠ABD,所以∠ABD=80°,再利用平行线的性质两直线平行,同旁内角互补,得出结论.
解答 解:∵AB∥CD,∠C=40°,
∴∠ABC=40°,
∵CB平分∠ABD,
∴∠ABD=80°,
∴∠D=100°.
故选B.
点评 本题主要考查了平行线的性质和角平分线的定义,利用两直线平行,内错角相等;两直线平行,同旁内角互补是解答此题的关键.

练习册系列答案
 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
11.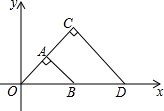 如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD.若B(1,0),则点C的坐标为( )
如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD.若B(1,0),则点C的坐标为( )
 如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD.若B(1,0),则点C的坐标为( )
如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD.若B(1,0),则点C的坐标为( )| A. | (1,2) | B. | (1,1) | C. | ($\sqrt{2}$,$\sqrt{2}$) | D. | (2,1) |
15.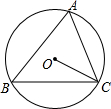 如图,⊙O为△ABC的外接圆,∠A=72°,则∠BCO的度数为( )
如图,⊙O为△ABC的外接圆,∠A=72°,则∠BCO的度数为( )
 如图,⊙O为△ABC的外接圆,∠A=72°,则∠BCO的度数为( )
如图,⊙O为△ABC的外接圆,∠A=72°,则∠BCO的度数为( )| A. | 15° | B. | 18° | C. | 20° | D. | 28° |
12.计算(a2)3的正确结果是( )
| A. | 3a2 | B. | a6 | C. | a5 | D. | 6a |
12.下列说法正确的是( )
| A. | 角的边越长,角度就越大 | B. | 周角就是一条射线 | ||
| C. | 一条直线可以看成平角 | D. | 平角的两边可以构成一条直线 |
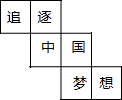 一个正方体的平面展开图如图所示,每一个面都有一个汉字,则在该正方体中和“国”字相对的汉字是( )
一个正方体的平面展开图如图所示,每一个面都有一个汉字,则在该正方体中和“国”字相对的汉字是( )


