题目内容
18.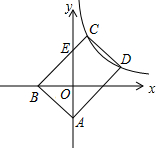 如图,平行四边形ABCD中A点的坐标为(0,-2),B在x轴的负半轴上,C、D两点落在反比例函数y=kx-1上,且D点的横坐标为3,四边形AECD的面积是三角形ABE面积的3倍.求k的值.
如图,平行四边形ABCD中A点的坐标为(0,-2),B在x轴的负半轴上,C、D两点落在反比例函数y=kx-1上,且D点的横坐标为3,四边形AECD的面积是三角形ABE面积的3倍.求k的值.
分析 先根据四边形AECD的面积是三角形ABE面积的3倍,结合平行四边形的性质得出E是BC的中点,B、C两点的横坐标互为相反数,设C点横坐标为x,则B点横坐标为-x.再由平行四边形ABCD中A点的坐标为(0,-2),D点的横坐标为3,求出x=1.5.设D(3,y),根据反比例函数图象上点的坐标特征得出C(1.5,2y),再利用平行四边形的性质求出y=2,D(3,2),那么k=3×2=6.
解答 解:∵四边形AECD的面积是三角形ABE面积的3倍,
∴三角形ABE的面积=$\frac{1}{4}$×平行四边形ABCD的面积=$\frac{1}{2}$×三角形ABC的面积,
∴E是BC的中点,
∵E在y轴上,横坐标是0,
∴B、C两点的横坐标互为相反数,设C点横坐标为x,则B点横坐标为-x.
∵平行四边形ABCD中A点的坐标为(0,-2),D点的横坐标为3,
∴x-(-x)=3-0,
∴x=1.5.
设D(3,y),
∵C、D两点落在反比例函数y=kx-1上,
∴C点纵坐标为$\frac{3y}{1.5}$=2y,即C(1.5,2y).
∵A(0,-2),B(-1.5,0),C(1.5,2y),D(3,y),且四边形ABCD是平行四边形,
∴2y-y=0-(-2),
∴y=2,
∴D(3,2),
∴k=3×2=6.
点评 本题考查了反比例函数比例系数k的几何意义,平行四边形的性质,反比例函数图象上点的坐标特征,求出B、C两点的横坐标是解题的关键.

练习册系列答案
相关题目
6.下列各式中,能用完全平方公式分解因式的是( )
| A. | 4x2-1 | B. | x2-x+0.25 | C. | x2-xy+y2 | D. | x2-8x-16 |
13.已知整式x2-2x的值为6,则代数式5-2x2+4x的值为( )
| A. | 8 | B. | -7 | C. | 11 | D. | -17 |
10.下列说法正确的是( )
| A. | $\frac{1}{3}$πx2的系数为$\frac{1}{3}$ | B. | $\frac{1}{2}$xy2的系数为$\frac{1}{2}$x | ||
| C. | -5x2y的次数为3 | D. | 32a2b2的次数为6 |
7.若直角三角形的两条直角边的长分别为5和12,则斜边上的中线长是( )
| A. | 6 | B. | 6.5 | C. | 13 | D. | 不能确定 |
8.如图,从边长为(a+4)的正方形中剪去一个边长为(a+1)的正方形(a>0),剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙),则矩形的周长为( )
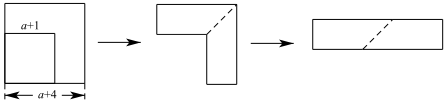

| A. | 4a+10 | B. | 4a+11 | C. | 4a+16 | D. | 以上答案都不对 |
 如图,分别是由若干个完全相同的小正方体组成的一个物体的主视图和俯视图,则组成这个物体的小正方体的个数至少4个.
如图,分别是由若干个完全相同的小正方体组成的一个物体的主视图和俯视图,则组成这个物体的小正方体的个数至少4个.