题目内容
如图 ,在正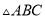 的内部,作
的内部,作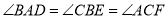 ,
, 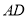 ,
, 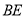 ,
, 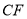 两两相交于
两两相交于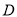 ,
, 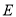 ,
, 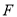 三点 (
三点 (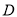 ,
, 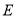 ,
, 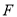 三点不重合).
三点不重合).
(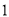 )
)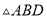 ,
, 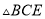 ,
, 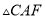 是否全等?如果是,请选择其中一对进行证明.
是否全等?如果是,请选择其中一对进行证明.
(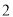 )
)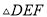 是否为正三角形?请说明理由.
是否为正三角形?请说明理由.
(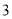 )进一步探究发现,
)进一步探究发现, 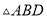 的三边存在一定的等量关系,设
的三边存在一定的等量关系,设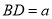 ,
, 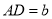 ,
, 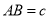 ,请探索
,请探索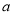 ,
, 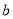 ,
, 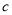 满足的等量关系.
满足的等量关系.
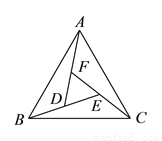
练习册系列答案
 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
题目内容
如图 ,在正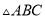 的内部,作
的内部,作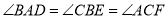 ,
, 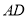 ,
, 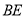 ,
, 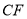 两两相交于
两两相交于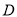 ,
, 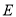 ,
, 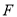 三点 (
三点 (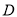 ,
, 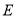 ,
, 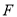 三点不重合).
三点不重合).
(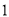 )
)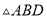 ,
, 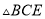 ,
, 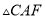 是否全等?如果是,请选择其中一对进行证明.
是否全等?如果是,请选择其中一对进行证明.
( )
)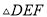 是否为正三角形?请说明理由.
是否为正三角形?请说明理由.
( )进一步探究发现,
)进一步探究发现, 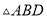 的三边存在一定的等量关系,设
的三边存在一定的等量关系,设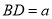 ,
, 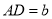 ,
, 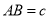 ,请探索
,请探索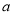 ,
, 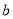 ,
, 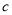 满足的等量关系.
满足的等量关系.
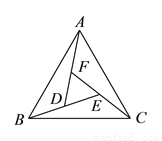
 同步拓展阅读系列答案
同步拓展阅读系列答案