题目内容
如图，已知DE是△ABC的中位线，F是DE的中点，CF的延长线交AB于点G，若DG=2，求AD的长．考点：三角形中位线定理,全等三角形的判定与性质
专题：
分析：过点E作EH∥CG与AB相交于点H，然后判断出GF是△DEH的中位线，EH是△ACG的中位线，再求出GH、AH，然后根据AD=AH+GH+DG计算即可得解．
解答：
解：如图，过点E作EH∥CG与AB相交于点H，
∵F是DE的中点，
∴GF是△DEH的中位线，EH是△ACG的中位线，
∴GH=DG=2，AH=DH=2，
∴AD=AH+GH+DG=2+2+2=6．
解：如图，过点E作EH∥CG与AB相交于点H，∵F是DE的中点，
∴GF是△DEH的中位线，EH是△ACG的中位线，
∴GH=DG=2，AH=DH=2，
∴AD=AH+GH+DG=2+2+2=6．
点评：本题考查了三角形的中位线定理，熟记定理是解题的关键，难点在于作出辅助线构造出含中位线的三角形．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
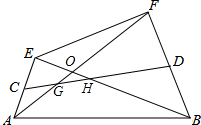已知四边形ABFE中AF=BE，C、D是AE、BF中点，求证：OG=OH．