题目内容
如图，在⊙O中，∠BOD=80°，求∠A和∠C的度数．考点：圆周角定理,圆内接四边形的性质
专题：
分析：先根据圆周角定理求出∠A的度数，再由圆内接四边形的性质得出∠C的度数即可．
解答：解：∵∠BOD与∠C是同弧所对的圆心角与圆周角，∠BOD=80°，
∴∠A=
×80°=40°．
∵四边形ABCD是圆内接四边形，
∴∠D=180°-∠A=180°-40°=140°．
∴∠A=
| 1 |
| 2 |
∵四边形ABCD是圆内接四边形，
∴∠D=180°-∠A=180°-40°=140°．
点评：本题考查的是圆周角定理，熟知在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半是解答此题的关键．
练习册系列答案
新思维假期作业暑假吉林大学出版社系列答案
蓝天教育暑假优化学习系列答案
相关题目
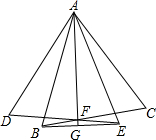如图，等边△ABC绕点A顺时针旋转到△ADE，BC与DE相交于点F，连接AF并延长，交BE于点G，求证：AF⊥BE．若
=
，则
的值等于（ ）
| a |
| b |
| 4 |
| 3 |
| a+b |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
如图，矩形AEHC是由三个全等矩形拼成的，AH与BE、BF、DF、DG、CG分别交于点P、Q、K、M、N．设△BPQ，△DKM，△CNH的面积依次为S1，S2，S3．若S1+S3=20，则S2的值为（ ）| A、6 | B、8 | C、10 | D、12 |
如图，已知△ABC中，∠C=90°，∠A=60°，a=15，根据定义求∠A，∠B的三角函数值．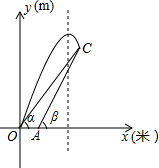
如图是某次军事演习迫击炮射击目标时在平面直角坐标系中的示意图，地面有O、A两个观测点，分别测得目标C的仰角为α、β，OA=20米，tan
如图，在⊙O的内接四边形ABCD中，∠BOD=120°，那么∠BCD是（ ）| A、120° | B、100° |
| C、80° | D、60° |