题目内容
18.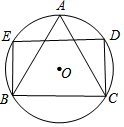 如图,⊙O的半径为1,△ABC是⊙O的内接等边三角形,点D、E在圆上,四边形BCDE为矩形,这个矩形的面积是( )
如图,⊙O的半径为1,△ABC是⊙O的内接等边三角形,点D、E在圆上,四边形BCDE为矩形,这个矩形的面积是( )| A. | 2 | B. | $\frac{3}{2}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
分析 连接BD、OC,根据矩形的性质得∠BCD=90°,再根据圆周角定理得BD为⊙O的直径,利用圆周角定理得到∠BOC=2∠A=120°,根据含30°的直角三角形三边的关系得到CD=$\frac{1}{2}$BD=1,BC=$\sqrt{3}$CD=$\sqrt{3}$,然后根据矩形的面积公式求解.
解答 解:连结BD、OC,如图,
∵四边形BCDE为矩形,
∴∠BCD=90°,
∴BD为⊙O的直径,
∴BD=2,
∵△ABC为等边三角形,
∴∠A=60°,
∴∠BOC=2∠A=120°,
而OB=OC,
∴∠CBD=30°,
在Rt△BCD中,CD=$\frac{1}{2}$BD=1,BC=$\sqrt{3}$CD=$\sqrt{3}$,
∴矩形BCDE的面积=BC•CD=$\sqrt{3}$.
故选:C.
点评 本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了圆周角定理、等边三角形的性质和矩形的性质.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
8.若顺次连接四边形的各边中点所得四边形为矩形,则该四边形一定是( )
| A. | 菱形 | B. | 平行四边形 | ||
| C. | 对角线相等的四边形 | D. | 对角线互相垂直的四边形 |
6.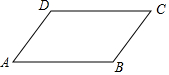 如图,若平行四边形ABCD中,AB=6,AD=4,∠B=150°,则平行四边形ABCD的面积为( )
如图,若平行四边形ABCD中,AB=6,AD=4,∠B=150°,则平行四边形ABCD的面积为( )
 如图,若平行四边形ABCD中,AB=6,AD=4,∠B=150°,则平行四边形ABCD的面积为( )
如图,若平行四边形ABCD中,AB=6,AD=4,∠B=150°,则平行四边形ABCD的面积为( )| A. | 6 | B. | 12 | C. | 12$\sqrt{3}$ | D. | 24 |
13.一个等腰三角形的两条边长分别是方程x2-3x+2=0的两根,则该等腰三角形的周长是( )
| A. | 5或4 | B. | 4 | C. | 5 | D. | 3 |
3.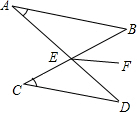 如图,已知AB∥CD,AD与BC相交于点E,EF平分∠BED,若∠A=30°,∠C=40°,则∠DEF的度数为( )
如图,已知AB∥CD,AD与BC相交于点E,EF平分∠BED,若∠A=30°,∠C=40°,则∠DEF的度数为( )
 如图,已知AB∥CD,AD与BC相交于点E,EF平分∠BED,若∠A=30°,∠C=40°,则∠DEF的度数为( )
如图,已知AB∥CD,AD与BC相交于点E,EF平分∠BED,若∠A=30°,∠C=40°,则∠DEF的度数为( )| A. | 70° | B. | 50° | C. | 35° | D. | 30° |
10.实数8的立方根是( )
| A. | -2 | B. | 2 | C. | -3 | D. | 3 |
8. 一个几何体的三视图如图所示,这个几何体是( )
一个几何体的三视图如图所示,这个几何体是( )
 一个几何体的三视图如图所示,这个几何体是( )
一个几何体的三视图如图所示,这个几何体是( )| A. | 球 | B. | 圆柱 | C. | 圆锥 | D. | 立方体 |
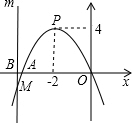 如图,已知抛物线l1的顶点是P(-2,4),且经过点O(0,0)、A(t,0),平行于y轴的直线m与x轴交于点B(b,0),与抛物线l1交于点M.
如图,已知抛物线l1的顶点是P(-2,4),且经过点O(0,0)、A(t,0),平行于y轴的直线m与x轴交于点B(b,0),与抛物线l1交于点M.