题目内容
6．
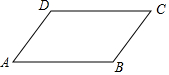如图，若平行四边形ABCD中，AB=6，AD=4，∠B=150°，则平行四边形ABCD的面积为（ ）| A． | 6 | B． | 12 | C． | 12$\sqrt{3}$ | D． | 24 |
分析 作平行四边形的高DE，由平行四边形的性质求出∠A=30°，由含30°角的直角三角形的性质求出DE，即可求出平行四边形的面积．
解答 解：作DE⊥AB于E，如图所示
∵四边形ABCD是平行四边形，
∴AD=BC=4，AD∥BC，
∴∠A+∠B=180°，
∴∠A=30°，
∴DE=$\frac{1}{2}$AD=2，
∴S?ABCD=AB•DE=6×2=12．
故选：B．
点评 本题考查了平行四边形的性质、含30°角的直角三角形的性质、平行四边形面积的计算；熟练掌握平行四边形的性质，求出AB边上的高DE是解决问题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，在Rt△ABC中，∠B=90°，分别以点A、C为圆心，大于$\frac{1}{2}$AC长为半径画弧，两弧相交于点M、N，作直线MN，与AC、BC分别交于点D、E，连接AE，当AB=3，AC=5时，△ABE的周长等于（ ）
17．计算（-6）+（-2）的结果等于（ ）
| A． | 8 | B． | -8 | C． | 12 | D． | -12 |
1．
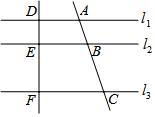如图，直线L1∥L2∥L3，直线AC分别交，L1，L2，L3于点A，B，C，直线DF分别交，L1，L2，L3于点D，E，F．若DE=3，EF=6，AB=4，则AC的长是（ ）
如图，直线L1∥L2∥L3，直线AC分别交，L1，L2，L3于点A，B，C，直线DF分别交，L1，L2，L3于点D，E，F．若DE=3，EF=6，AB=4，则AC的长是（ ）| A． | 6 | B． | 8 | C． | 9 | D． | 12 |
11．
随着移动互联网的快速发展，OFO、摩拜等互联网共享单车应运而生并快速发展．小冬骑的摩拜单车，爸爸骑的摩托车，沿相同路线由A地到B地，行驶过程中路程y和时间x的函数关系的图象如图，根据图象分析，何时俩人相遇，谁先到（ ）
随着移动互联网的快速发展，OFO、摩拜等互联网共享单车应运而生并快速发展．小冬骑的摩拜单车，爸爸骑的摩托车，沿相同路线由A地到B地，行驶过程中路程y和时间x的函数关系的图象如图，根据图象分析，何时俩人相遇，谁先到（ ）| A． | 4分钟时相遇，爸爸先到 | B． | 20分钟时相遇，爸爸先到 | ||
| C． | 4分时相遇，小冬先到 | D． | 20分钟时相遇，小冬先到 |
18．
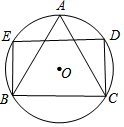如图，⊙O的半径为1，△ABC是⊙O的内接等边三角形，点D、E在圆上，四边形BCDE为矩形，这个矩形的面积是（ ）
如图，⊙O的半径为1，△ABC是⊙O的内接等边三角形，点D、E在圆上，四边形BCDE为矩形，这个矩形的面积是（ ）| A． | 2 | B． | $\frac{3}{2}$ | C． | $\sqrt{3}$ | D． | $\frac{\sqrt{3}}{2}$ |
15．
如图，某同学家在A处，现在该同学要去位于B处的同学家去玩，请帮助他选择一条最近的路线（ ）
如图，某同学家在A处，现在该同学要去位于B处的同学家去玩，请帮助他选择一条最近的路线（ ）| A． | A→C→D→B | B． | A→C→F→B | C． | A→C→E→F→B | D． | A→C→M→B |