题目内容
7.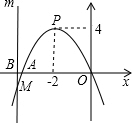 如图,已知抛物线l1的顶点是P(-2,4),且经过点O(0,0)、A(t,0),平行于y轴的直线m与x轴交于点B(b,0),与抛物线l1交于点M.
如图,已知抛物线l1的顶点是P(-2,4),且经过点O(0,0)、A(t,0),平行于y轴的直线m与x轴交于点B(b,0),与抛物线l1交于点M.(1)求t的值及抛物线l1的解析式;
(2)当BM=4时,求b的值;
(3)把抛物线l1绕点(0,1)旋转180°,得到抛物线l2.
①直接写出当两条抛物线对应的函数值y都随着x的增大而减小时,x的取值范围.
②直线m与抛物线l2交于点N,设线段MN的长为n,求n与b的关系式,并求出线段MN的最小值及此时b的值.
分析 (1)先利用抛物线的顶点坐标求出t的值,进而用待定系数法求出抛物线解析式;
(2)先确定出BM=4,再分两种情况,利用点M的纵坐标建立方程求解即可;
(3)先表示出点M,N的坐标,进而确定出n与b的函数关系式,即可得出结论.
解答 解:(1)∵抛物线l1的顶点是P(-2,4),
∴对称轴为x=-2,
∴A(-4,0),
∴t=-4,
设抛物线l1的解析式为y=a(x+2)2+4,
∵抛物线过点O,
∴4a+4=0,
∴a=-1,
∴抛物线l1的解析式为y=-(x+2)2+4,
(2)∵点M在抛物线l1上,
∴点B在x轴上,且BM=4,
①当点M在x轴下方时,M(b,-4),
∴-4=(b+2)2+4,
∴b=2±2$\sqrt{2}$,
②当点M在x轴上方时,M(b,4),
∴4=-(b+2)2,
∴b=-2,
∴当BM=4时,b=-2或-2+2$\sqrt{2}$或-2-2$\sqrt{2}$;
(3)① ,
,
由图象知,-2<x<2,
②∵点P关于(0,1)的对称点为P'(2,-2),
∴抛物线l2的解析式为y=(x-2)2-2,
设点M(b,-(b+2)2+4),∴N(b,(b-2)2-2),
∴MN=n=(b-2)2-2-[-(b+2)2+4]=2b2+2,
∴当b=0时,MN的最小值为2.
点评 此题是二次函数综合题,主要考查了待定系数法,对称的性质,解本题的关键是用方程的思想解决问题,是一道基础题目.

练习册系列答案
相关题目
17.计算(-6)+(-2)的结果等于( )
| A. | 8 | B. | -8 | C. | 12 | D. | -12 |
18.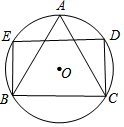 如图,⊙O的半径为1,△ABC是⊙O的内接等边三角形,点D、E在圆上,四边形BCDE为矩形,这个矩形的面积是( )
如图,⊙O的半径为1,△ABC是⊙O的内接等边三角形,点D、E在圆上,四边形BCDE为矩形,这个矩形的面积是( )
 如图,⊙O的半径为1,△ABC是⊙O的内接等边三角形,点D、E在圆上,四边形BCDE为矩形,这个矩形的面积是( )
如图,⊙O的半径为1,△ABC是⊙O的内接等边三角形,点D、E在圆上,四边形BCDE为矩形,这个矩形的面积是( )| A. | 2 | B. | $\frac{3}{2}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
15. 如图,某同学家在A处,现在该同学要去位于B处的同学家去玩,请帮助他选择一条最近的路线( )
如图,某同学家在A处,现在该同学要去位于B处的同学家去玩,请帮助他选择一条最近的路线( )
 如图,某同学家在A处,现在该同学要去位于B处的同学家去玩,请帮助他选择一条最近的路线( )
如图,某同学家在A处,现在该同学要去位于B处的同学家去玩,请帮助他选择一条最近的路线( )| A. | A→C→D→B | B. | A→C→F→B | C. | A→C→E→F→B | D. | A→C→M→B |
2. 如图,点A的坐标为(3,$\sqrt{7}$),点B的坐标为(6,0),将△AOB绕点B按顺时针方向旋转一定的角度后得到△A'O'B,点A的对应点A'在x轴上,则点O'的坐标为( )
如图,点A的坐标为(3,$\sqrt{7}$),点B的坐标为(6,0),将△AOB绕点B按顺时针方向旋转一定的角度后得到△A'O'B,点A的对应点A'在x轴上,则点O'的坐标为( )
 如图,点A的坐标为(3,$\sqrt{7}$),点B的坐标为(6,0),将△AOB绕点B按顺时针方向旋转一定的角度后得到△A'O'B,点A的对应点A'在x轴上,则点O'的坐标为( )
如图,点A的坐标为(3,$\sqrt{7}$),点B的坐标为(6,0),将△AOB绕点B按顺时针方向旋转一定的角度后得到△A'O'B,点A的对应点A'在x轴上,则点O'的坐标为( )| A. | ($\frac{9}{2}$,$\frac{3}{2}\sqrt{7}$) | B. | ($\frac{21}{2}$,$\frac{3}{2}\sqrt{7}$) | C. | ($\frac{21}{2}$,$\frac{3}{2}\sqrt{5}$) | D. | ($\frac{25}{2}$,$\frac{3}{2}$$\sqrt{5}$) |
19.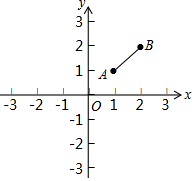 如图,在平面直角坐标系xOy中,A(1,1),B(2,2),双曲线y=$\frac{k}{x}$与线段AB有公共点,则k的取值范围是( )
如图,在平面直角坐标系xOy中,A(1,1),B(2,2),双曲线y=$\frac{k}{x}$与线段AB有公共点,则k的取值范围是( )
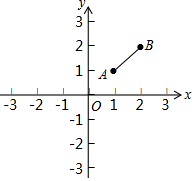 如图,在平面直角坐标系xOy中,A(1,1),B(2,2),双曲线y=$\frac{k}{x}$与线段AB有公共点,则k的取值范围是( )
如图,在平面直角坐标系xOy中,A(1,1),B(2,2),双曲线y=$\frac{k}{x}$与线段AB有公共点,则k的取值范围是( )| A. | k>0 | B. | k≥1 | C. | k≥4 | D. | 1≤k≤4 |
17.如图所示,将形状、大小完全相同的“●”和线段按照一定规律摆成下列图形,第1幅图形中“●”的个数为a1,第2幅图形中“●”的个数为a2,第3幅图形中“●”的个数为a3,…,以此类推,则$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+$\frac{1}{{a}_{3}}$+…+$\frac{1}{{a}_{19}}$的值为( )
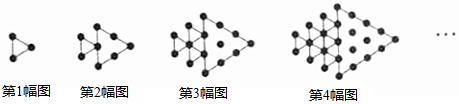

| A. | $\frac{20}{21}$ | B. | $\frac{61}{84}$ | C. | $\frac{589}{840}$ | D. | $\frac{431}{760}$ |
 如图所示是8个完全相同的小正方体组成的几何体,则该几何体的左视图是( )
如图所示是8个完全相同的小正方体组成的几何体,则该几何体的左视图是( )


