题目内容
13.已知ab>0,bc<0,则直线y=-$\frac{a}{b}$x+$\frac{a}{c}$经过的象限为( )| A. | 一、二、三 | B. | 一、二、四 | C. | 二、三、四 | D. | 一、二、四 |
分析 根据ab>0,bc<0得到直线的比例系数的符号,然后根据一次函数的性质确定正确的选项即可.
解答 解:∵ab>0,bc<0,
∴ab同号,bc异号,ac异号,
∴y=-$\frac{a}{b}$x+$\frac{a}{c}$中-$\frac{a}{b}$<0,$\frac{a}{c}$<0,
∴一次函数y=-$\frac{a}{b}$x+$\frac{a}{c}$经过二、三、四象限,
故选C.
点评 本题考查了一次函数的图象与系数的关系,解题的关键是能够确定比例系数的符号,难度不大.

练习册系列答案
相关题目
18.一个数除以9的商为x,余数为2,则这个数为( )
| A. | 9x+2 | B. | 9x-2 | C. | -$\frac{2}{9}$x | D. | $\frac{2}{9}$x |
2.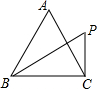 如图,在边长为3的等边△ABC中,过点C作垂直于BC的直线交∠ABC的平分线于点P,则点P到边AB所在直线的距离为( )
如图,在边长为3的等边△ABC中,过点C作垂直于BC的直线交∠ABC的平分线于点P,则点P到边AB所在直线的距离为( )
 如图,在边长为3的等边△ABC中,过点C作垂直于BC的直线交∠ABC的平分线于点P,则点P到边AB所在直线的距离为( )
如图,在边长为3的等边△ABC中,过点C作垂直于BC的直线交∠ABC的平分线于点P,则点P到边AB所在直线的距离为( )| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
3.一个各面分别标有数字1,2,3,4,5,6的骰子,连续投掷二次,分别出现数字m,n,得到一个点P(m,n),则点P既在直线y=-x+5上,又在双曲线y=$\frac{6}{x}$上的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{9}$ | C. | $\frac{1}{18}$ | D. | $\frac{1}{36}$ |
 如图,已知抛物线y=ax2+bx-3与直线y=x交于A,B两点,且A,B两点的横坐标分别为-1和3.
如图,已知抛物线y=ax2+bx-3与直线y=x交于A,B两点,且A,B两点的横坐标分别为-1和3. 小明想把一长为25cm,宽为20cm的长方形硬纸片做成一个无盖的长方体盒子,于是在长方形纸片的四个角各剪去一个相同的小正方形.
小明想把一长为25cm,宽为20cm的长方形硬纸片做成一个无盖的长方体盒子,于是在长方形纸片的四个角各剪去一个相同的小正方形. 如图,
如图,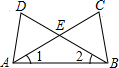 如图,∠1=∠2,∠C=∠D,AC、BD交于E点,下列结论中正确的有( )
如图,∠1=∠2,∠C=∠D,AC、BD交于E点,下列结论中正确的有( )