题目内容
17.圆内接正六边形的边心距为2$\sqrt{3}$cm,则这个正六边形的面积为24$\sqrt{3}$cm2.分析 根据正六边形的特点,通过中心作边的垂线,连接半径,结合解直角三角形的有关知识解决.
解答 解:如图,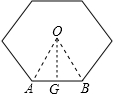
连接OA、OB;过点O作OG⊥AB于点G.
在Rt△AOG中,OG=2$\sqrt{3}$,∠AOG=30°,
∵OG=OA•cos 30°,
∴OA=$\frac{OG}{cos30°}$=$\frac{2\sqrt{3}}{\frac{\sqrt{3}}{2}}$=4cm,
∴这个正六边形的面积为6×$\frac{1}{2}$×4×2$\sqrt{3}$=24$\sqrt{3}$cm2.
故答案为:24$\sqrt{3}$.
点评 此题主要考查正多边形的计算问题,根据题意画出图形,再根据正多边形的性质及锐角三角函数的定义解答即可.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
12.若关于x的分式方程$\frac{2}{x-3}$+$\frac{x+m}{3-x}$=2有增根,则m的值是( )
| A. | m=-1 | B. | m=0 | C. | m=3 | D. | m=0或m=3 |
7.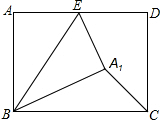 如图,在矩形ABCD中,AB=5,BC=7,点E是AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A′恰好落在∠BCD的平分线上时,CA′的长为( )
如图,在矩形ABCD中,AB=5,BC=7,点E是AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A′恰好落在∠BCD的平分线上时,CA′的长为( )
 如图,在矩形ABCD中,AB=5,BC=7,点E是AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A′恰好落在∠BCD的平分线上时,CA′的长为( )
如图,在矩形ABCD中,AB=5,BC=7,点E是AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A′恰好落在∠BCD的平分线上时,CA′的长为( )| A. | 3或4$\sqrt{2}$ | B. | 3$\sqrt{2}$或4$\sqrt{2}$ | C. | 3或4 | D. | 4或3$\sqrt{2}$ |
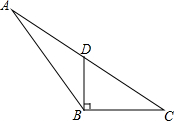 如图,在△ABC中,D为AC边的中点,且DB⊥BC,BC=4,CD=5.
如图,在△ABC中,D为AC边的中点,且DB⊥BC,BC=4,CD=5.
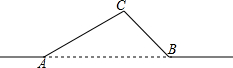 如图,一条输电线路从A地到B地需要经过C地,图中AC=20千米,∠CAB=30°,∠CBA=45°,因线路整改需要,将从A地到B地之间铺设一条笔直的输电线路.
如图,一条输电线路从A地到B地需要经过C地,图中AC=20千米,∠CAB=30°,∠CBA=45°,因线路整改需要,将从A地到B地之间铺设一条笔直的输电线路.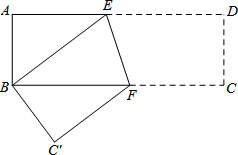 如图,在矩形纸片ABCD中,AB=4cm,AD=8cm,按如图方式折叠,使点D与点B重合,折痕为EF,则tan∠BEF=( )
如图,在矩形纸片ABCD中,AB=4cm,AD=8cm,按如图方式折叠,使点D与点B重合,折痕为EF,则tan∠BEF=( )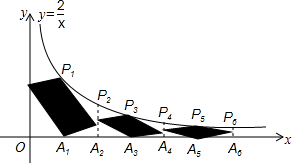 如图,在反比例函数y=$\frac{2}{x}$(x>0)的图象上有点P1,P2,P3,…,它们的横坐标依次为1,2,3,…,分别过这些点作x轴的垂线,垂足依次为A1,A2,A3,…,分别以P1A1,P3A3,P5A5…为对角线作平行四边形,另两顶点分别落在P2n-2A2n-2与P2nA2n上(n=1,2,3,…,P0A0为y轴),所构成的阴影部分的面积从左到右依次为S1,S2,S3,…,记P1=$\frac{1}{{S}_{1}}$,P2=$\frac{1}{{S}_{1}}$+$\frac{1}{{S}_{2}}$,P3=$\frac{1}{{S}_{1}}$+$\frac{1}{{S}_{2}}$+$\frac{1}{{S}_{3}}$,…,则P2=2;Pn-Pn-1=$\frac{2n-1}{2}$.
如图,在反比例函数y=$\frac{2}{x}$(x>0)的图象上有点P1,P2,P3,…,它们的横坐标依次为1,2,3,…,分别过这些点作x轴的垂线,垂足依次为A1,A2,A3,…,分别以P1A1,P3A3,P5A5…为对角线作平行四边形,另两顶点分别落在P2n-2A2n-2与P2nA2n上(n=1,2,3,…,P0A0为y轴),所构成的阴影部分的面积从左到右依次为S1,S2,S3,…,记P1=$\frac{1}{{S}_{1}}$,P2=$\frac{1}{{S}_{1}}$+$\frac{1}{{S}_{2}}$,P3=$\frac{1}{{S}_{1}}$+$\frac{1}{{S}_{2}}$+$\frac{1}{{S}_{3}}$,…,则P2=2;Pn-Pn-1=$\frac{2n-1}{2}$.