题目内容
7.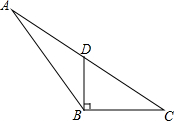 如图,在△ABC中,D为AC边的中点,且DB⊥BC,BC=4,CD=5.
如图,在△ABC中,D为AC边的中点,且DB⊥BC,BC=4,CD=5.(1)求DB的长;
(2)在△ABC中,求BC边上高的长.
分析 (1)直接利用勾股定理得出BD的长即可;
(2)利用平行线分线段成比例定理得出BD=$\frac{1}{2}$AE,进而求出即可.
解答  解:(1)∵DB⊥BC,BC=4,CD=5,
解:(1)∵DB⊥BC,BC=4,CD=5,
∴BD=$\sqrt{{5}^{2}-{4}^{2}}$=3;
(2)延长CB,过点A作AE⊥CB延长线于点E,
∵DB⊥BC,AE⊥BC,
∴AE∥DB,
∵D为AC边的中点,
∴BD=$\frac{1}{2}$AE,
∴AE=6,即BC边上高的长为6.
点评 此题主要考查了勾股定理以及平行线分线段成比例定理,得出BD=$\frac{1}{2}$AE是解题关键.

练习册系列答案
相关题目
15. 过矩形ABCD的对角线AC的中点O作EF⊥AC,交BC边于点E,交AD边于点F,分别连接AE、CF.若AB=$\sqrt{3}$,∠DCF=30°,则EF的长为( )
过矩形ABCD的对角线AC的中点O作EF⊥AC,交BC边于点E,交AD边于点F,分别连接AE、CF.若AB=$\sqrt{3}$,∠DCF=30°,则EF的长为( )
 过矩形ABCD的对角线AC的中点O作EF⊥AC,交BC边于点E,交AD边于点F,分别连接AE、CF.若AB=$\sqrt{3}$,∠DCF=30°,则EF的长为( )
过矩形ABCD的对角线AC的中点O作EF⊥AC,交BC边于点E,交AD边于点F,分别连接AE、CF.若AB=$\sqrt{3}$,∠DCF=30°,则EF的长为( )| A. | 2 | B. | 3 | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
2. 如图,图中∠1的大小等于( )
如图,图中∠1的大小等于( )
 如图,图中∠1的大小等于( )
如图,图中∠1的大小等于( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
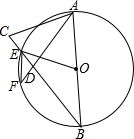 如图,等腰三角形ABC中,BA=BC,以AB为直径作圆,交BC于点E,圆心为O.在EB上截取ED=EC,连接AD并延长,交⊙O于点F,连接OE、EF.
如图,等腰三角形ABC中,BA=BC,以AB为直径作圆,交BC于点E,圆心为O.在EB上截取ED=EC,连接AD并延长,交⊙O于点F,连接OE、EF.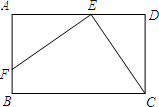 如图,已知矩形ABCD中,E是AD上的一点,F是AB上的一点,EF⊥EC,且EF=EC,DE=4cm,矩形ABCD的周长为32cm,则AE的长为6cm.
如图,已知矩形ABCD中,E是AD上的一点,F是AB上的一点,EF⊥EC,且EF=EC,DE=4cm,矩形ABCD的周长为32cm,则AE的长为6cm.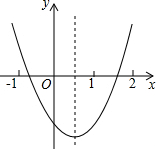 如图,观察二次函数y=ax2+bx+c的图象,下列结论:
如图,观察二次函数y=ax2+bx+c的图象,下列结论: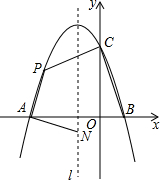 如图,抛物线y=ax2+bx+c与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴l为x=-1.
如图,抛物线y=ax2+bx+c与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴l为x=-1.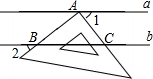 如图,直线a∥b,三角板的直角顶点A落在直线a上,两边分别交直线b于B、C两点.若∠1=42°,则∠2的度数是48°.
如图,直线a∥b,三角板的直角顶点A落在直线a上,两边分别交直线b于B、C两点.若∠1=42°,则∠2的度数是48°.