题目内容
5.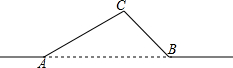 如图,一条输电线路从A地到B地需要经过C地,图中AC=20千米,∠CAB=30°,∠CBA=45°,因线路整改需要,将从A地到B地之间铺设一条笔直的输电线路.
如图,一条输电线路从A地到B地需要经过C地,图中AC=20千米,∠CAB=30°,∠CBA=45°,因线路整改需要,将从A地到B地之间铺设一条笔直的输电线路.(1)求新铺设的输电线路AB的长度;(结果保留根号)
(2)问整改后从A地到B地的输电线路比原来缩短了多少千米?(结果保留根号)
分析 (1)过C作CD⊥AB,交AB于点D,在直角三角形ACD中,利用锐角三角函数定义求出CD与AD的长,在直角三角形BCD中,利用锐角三角函数定义求出BD的长,由AD+DB求出AB的长即可;
(2)在直角三角形BCD中,利用勾股定理求出BC的长,由AC+CB-AB即可求出输电线路比原来缩短的千米数.
解答 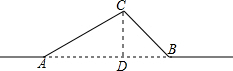 解:(1)过C作CD⊥AB,交AB于点D,
解:(1)过C作CD⊥AB,交AB于点D,
在Rt△ACD中,CD=AC•sin∠CAD=20×$\frac{1}{2}$=10(千米),AD=AC•cos∠CAD=20×$\frac{\sqrt{3}}{2}$=10$\sqrt{3}$(千米),
在Rt△BCD中,BD=$\frac{CD}{tan∠CBD}$=$\frac{10}{1}$=10(千米),
∴AB=AD+DB=10$\sqrt{3}$+10=10($\sqrt{3}$+1)(千米),
则新铺设的输电线路AB的长度10($\sqrt{3}$+1)(千米);
(2)在Rt△BCD中,根据勾股定理得:BC=$\sqrt{C{D}^{2}+B{D}^{2}}$=10$\sqrt{2}$(千米),
∴AC+CB-AB=20+10$\sqrt{2}$-(10$\sqrt{3}$+10)=10(1+$\sqrt{2}$-$\sqrt{3}$)(千米),
则整改后从A地到B地的输电线路比原来缩短了10(1+$\sqrt{2}$-$\sqrt{3}$)千米.
点评 此题考查了解直角三角形的应用,涉及的知识有:锐角三角函数定义,勾股定理,熟练掌握勾股定理是解本题的关键.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
15. 过矩形ABCD的对角线AC的中点O作EF⊥AC,交BC边于点E,交AD边于点F,分别连接AE、CF.若AB=$\sqrt{3}$,∠DCF=30°,则EF的长为( )
过矩形ABCD的对角线AC的中点O作EF⊥AC,交BC边于点E,交AD边于点F,分别连接AE、CF.若AB=$\sqrt{3}$,∠DCF=30°,则EF的长为( )
 过矩形ABCD的对角线AC的中点O作EF⊥AC,交BC边于点E,交AD边于点F,分别连接AE、CF.若AB=$\sqrt{3}$,∠DCF=30°,则EF的长为( )
过矩形ABCD的对角线AC的中点O作EF⊥AC,交BC边于点E,交AD边于点F,分别连接AE、CF.若AB=$\sqrt{3}$,∠DCF=30°,则EF的长为( )| A. | 2 | B. | 3 | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
13.在等腰三角形、平行四边形、直角梯形和圆中,既是轴对称图形又是中心对称图形的是( )
| A. | 等腰三角形 | B. | 平行四边形 | C. | 直角梯形 | D. | 圆 |
10.下列计算正确的是( )
| A. | |-2|=-2 | B. | a2•a3=a6 | C. | (-3)-2=$\frac{1}{9}$ | D. | $\sqrt{12}$=3$\sqrt{2}$ |
15.若代数式2x2+3x-3的值为11,则代数式6x2+9x+2013的值为( )
| A. | 2002 | B. | 2013 | C. | 2024 | D. | 2055 |
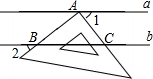 如图,直线a∥b,三角板的直角顶点A落在直线a上,两边分别交直线b于B、C两点.若∠1=42°,则∠2的度数是48°.
如图,直线a∥b,三角板的直角顶点A落在直线a上,两边分别交直线b于B、C两点.若∠1=42°,则∠2的度数是48°.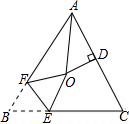 如图,△ABC中,AB=AC,∠BAC=64°,∠BAC的平分线与AC的垂直平分线交于点O,将∠B沿EF(E在BC上,F在AB上)折叠,点B与点O恰好重合,则∠OEB为( )度.
如图,△ABC中,AB=AC,∠BAC=64°,∠BAC的平分线与AC的垂直平分线交于点O,将∠B沿EF(E在BC上,F在AB上)折叠,点B与点O恰好重合,则∠OEB为( )度.