题目内容
18．已知AD是△ABC的一条中线，AB=9，AC=7，则AD的取值范围是（ ）| A． | 7＜AD＜9 | B． | 2＜AD＜16 | C． | 1＜AD＜8 | D． | 7＜AD＜8 |
分析 根据题意画出图形，延长AD至E，使DE=AD，连接CE．根据SAS证明△ABD≌△ECD，得CE=AB，再根据三角形的三边关系即可求解．
解答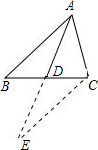 
解：延长AD至E，使DE=AD，连接CE．
∵BD=CD，∠ADB=∠EDC，AD=DE，
∴△ABD≌△ECD，
∴CE=AB．
在△ACE中，CE-AC＜AE＜CE+AC，
即2＜2AD＜16，
∴1＜AD＜8．
故选C．
点评 本题考查的是三角形的三边关系，根据题意画出图形，利用数形结合求解是解答此题的关键．
练习册系列答案
相关题目
9．下列关于二次函数的说法错误的是（ ）
| A． | 抛物线y=-2x2+3x+1的对称轴是直线x=$\frac{3}{4}$ | |
| B． | 点A（3，0）不在抛物线y=x2-2x-3的图象上 | |
| C． | 二次函数y=（x+2）2-2的顶点坐标是（-2，-2） | |
| D． | 函数y=2x2+4x-3的图象的最低点在（-1，-5） |
13．估计$\sqrt{32}$×$\sqrt{\frac{1}{4}}$+$\sqrt{18}$的运算结果应在（ ）
| A． | 5到6之间 | B． | 6到7之间 | C． | 7到8之间 | D． | 8到9之间 |
3．若$\sqrt{x-1}$+（y+3）2=0，则x-y的值为（ ）
| A． | 1 | B． | -1 | C． | 4 | D． | -7 |
10．下列各数属于正数的是（ ）
| A． | 0 | B． | -1.2 | C． | -5 | D． | 7 |