题目内容
4.解方程组$\left\{\begin{array}{l}{{x}^{2}-2xy+{y}^{2}=9①}\\{(x+y)^{2}-5(x+y)+6=0②}\end{array}\right.$.分析 分析:把方程①中用平方法转化为两个二元一次方程x-y=3或x-y=-3,方程②用因式分解法转化为两个二元一次方程x+y-2=0或x+y-3=0,最后原方程组转化为四个二元一次方程组来求解.
解答 解:由方程①得x-y=±3,
∴x-y=3或x-y=-3
由方程②,得(x+y-2)(x+y-3)=0,
∴x+y-2=0或x+y-3=0,
∴原方程组可化为$\left\{\begin{array}{l}{x-y=3}\\{x+y-2=0}\end{array}\right.$,$\left\{\begin{array}{l}{x-y=3}\\{x+y-3=0}\end{array}\right.$,$\left\{\begin{array}{l}{x-y=-3}\\{x+y-2=0}\end{array}\right.$,$\left\{\begin{array}{l}{x-y=-3}\\{x+y-3=0}\end{array}\right.$.
所以原方程组的解为:$\left\{\begin{array}{l}{x=\frac{5}{2}}\\{y=-\frac{1}{2}}\end{array}\right.$,$\left\{\begin{array}{l}{x=3}\\{y=0}\end{array}\right.$,$\left\{\begin{array}{l}{x=-\frac{1}{2}}\\{y=\frac{5}{2}}\end{array}\right.$,$\left\{\begin{array}{l}{x=0}\\{y=3}\end{array}\right.$
点评 本题考查了高次方程.关键是将方程组中的某个方程左边因式分解,使其积为0或两边开平方,可将较复杂的高次方程组转化为简单的高次方程组或者一次方程组来求解.

 阅读快车系列答案
阅读快车系列答案| A. | 两组对边分别相等 | B. | 两组对边分别平行 | ||
| C. | 对角线相等 | D. | 对角线互相平分 |

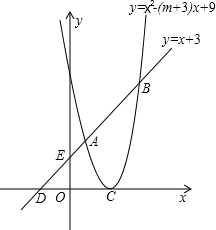 如图,已知抛物线y=x2-(m+3)x+9的顶点C在x轴正半轴上,一次函数y=x+3与抛物线交于A、B两点,与x、y轴分别交于D、E两点.
如图,已知抛物线y=x2-(m+3)x+9的顶点C在x轴正半轴上,一次函数y=x+3与抛物线交于A、B两点,与x、y轴分别交于D、E两点.