题目内容

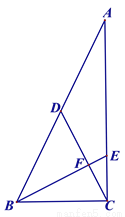
如图，在ΔABC中，∠ACB=90°，D是AB上一点，且BD=AD=CD,过B作BE⊥CD,分别交AC于点E、交CD于点F.

(1)求证：∠A=∠EBC;

(2)如果AC=2BC,请猜想BE和CD的数量关系，并证明你的猜想.

（1）证明见解析；(2)CD=BE,证明见解析. 【解析】试题分析：（1）由与∠ACB=90°得，∠ACD+∠BCD=90°和∠EBC+∠BCE=90°可得∠ACD=∠EBC，由CD=AD得∠DAC=∠ACD，从而得证； （2）过D作DG⊥AC于G，根据已知条件可证明CG=BC.再证明，即可得解 试题解析：（1） (2)CD=BE 过D作DG⊥AC于G 在ΔDG...
练习册系列答案
相关题目

不等式的正整数解有（　　）．

A. 1个 B. 2个 C. 3个 D. 4个

C 【解析】先求出不等式的解集，在取值范围内可以找到整数解． 【解析】 不等式的解集为x＜4； 正整数解为1，2，3，共3个． 故选C． 解答此题要先求出不等式的解集，再确定正整数解．求不等式组的解集，应遵循以下原则：同大取较大，同小取较小，小大大小中间找，大大小小解不了．

在同一直角坐标系中，二次函数y=﹣x2+m与一次函数y=mx﹣1（m≠0）的图象可能是（　　）

A. B.

C. D.

C 【解析】试题分析: 根据二次函数性质判断y＝－x2＋m开口向下,所以B错误,A、C、D三个选项中顶点坐标均在y轴的正半轴，说明m>0,所以可判断一次函数y＝mx－1过一、三、四象限，故选C.

若二次函数y=ax2的图象经过点P(－2，4)，则该图象必经过点（ ）

A. (2，4) B. (－2，－4) C. (－4，2) D. (4，－2)

A 【解析】试题分析：将点P代入解析式可得：a=1，即函数解析式为y=，则羡慕四个点只有A符合解析式.

抛物线y＝ax2，y＝bx2，y＝cx2的图象如图所示，则a，b，c的大小关系是________．

a＞b＞c 【解析】试题分析：抛物线图象开口方向由a得正负决定，a为正开口向上，a为负开口向下.抛物线图象开口的大小由决定， 越大，开口越小， 越小，开口越大.所以根据图象可以判断a>0，b<0,c<0, <,所以b>c.故答案为a＞b＞c.

计算：

（1）

（2）

(1) ;(2)-7- 【解析】试题分析：（1）先把各二次根式化为最简二次根式，然后合并即可； （2）根据二次根式的乘法法则运算； 试题解析：（1）原式= = =； （2） =2- =-7-

在实数范围内因式分解______________________ .

【解析】试题解析：∵x2-x-1=0的解为：x=， ∴x2-x-1=.

先化简，再求代数式÷﹣的值，其中x=4sin60°﹣2．

， 【解析】试题分析：先将分式的除法转化为乘法，同时将x2－2x＋1利用完全平方公式分解因式，约分化简后，再进行分式的减法运算，得出最简结果后，将化简后的x值代入计算即可． 试题解析： 【解析】 ＋ － = = = ， 当x=4sin60°－2=4×= －2时， 原式= ．

若a = （－0.4）2，b = －4－2，c =，d =， 则 a、b、c、d 的大小关系为（ ）

A. a<b<c<d B. b<a<d<c C. a<d<c<b D. c<a<d<b

B 【解析】∵a=0.16；b=-=-；c =()=16；d =1； 故：b