题目内容
8. 已知直线y=-$\frac{4}{3}$x+4与x轴和y轴分别交于B、A两点,另一直线经过点B和点D(11,6).
已知直线y=-$\frac{4}{3}$x+4与x轴和y轴分别交于B、A两点,另一直线经过点B和点D(11,6).(1)求A、B的坐标;
(2)求直线BD的解析式;
(3)证明:△ABD是直角三角形.
分析 (1)分别令函数解析式中x=0、y=0,求出对应的y、x的值,即可得出点A、B的坐标;
(2)结合点B、D的坐标,利用待定系数法即可求出直线BD的解析式;
(3)过点D作DM⊥y轴于点M,根据勾股定理求出AD2和AB2,由两点间的距离公式求出BD2,即可得出三者满足AD2=AB2+BD2,从而证得△ABD是直角三角形.
解答 解:(1)令y=-$\frac{4}{3}$x+4中x=0,则y=4,
∴点A(0,4);
令y=-$\frac{4}{3}$x+4中y=0,则-$\frac{4}{3}$x+4=0,解得:x=3,
∴点B(3,0).
(2)设直线BD的解析式为y=kx+b,
将点B(3,0)、D(11,6)代入y=kx+b中,
得:$\left\{\begin{array}{l}{3k+b=0}\\{11k+b=6}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=\frac{3}{4}}\\{b=-\frac{9}{4}}\end{array}\right.$,
∴直线BD的解析式为y=$\frac{3}{4}$x-$\frac{9}{4}$.
(3)证明:过点D作DM⊥y轴于点M,如图所示.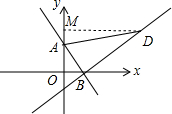
∵点A(0,4),点B(3,0),点D(11,6),
∴DM=11,OB=3,OA=4,AM=6-4=2,
由勾股定理可得:AD2=DM2+AM2=125,AB2=OA2+OB2=25,
又∵BD2=(11-3)2+(6-0)2=100,
∴AD2=AB2+BD2,
∴△ABD是直角三角形.
点评 本题考查了一次函数图象上点的坐标特征、待定系数法求函数解析式、勾股定理以及直角三角形的判定,解题的关键是:(1)分别代入x=0、y=0;(2)利用待定系数法求出函数解析式;(3)找出AD2=AB2+BD2.本题属于中档题,难度不大,解决该题型题目时,找出点的坐标,利用待定系数法求出函数解析式是关键.

 阅读快车系列答案
阅读快车系列答案| A. | m<1 | B. | m<0 | C. | m>0 | D. | m>1 |
| A. | 18 | B. | 15 | C. | 15或18 | D. | 19 |
| A. | 2x=3y+4 | B. | x=$\frac{3}{2}$y+2 | C. | 3y=2x-4 | D. | y=$\frac{2x-4}{3}$ |
| A. | x>-1 | B. | x<-1 | C. | x>1 | D. | x>0 |
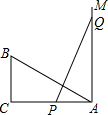 如图,∠C=∠CAM=90°,AC=8,BC=4,P、Q两点分别在线段AC和射线AM上运动,且PQ=AB.若△ABC与△PQA全等,则AP的长度为8或4.
如图,∠C=∠CAM=90°,AC=8,BC=4,P、Q两点分别在线段AC和射线AM上运动,且PQ=AB.若△ABC与△PQA全等,则AP的长度为8或4. 如图,△ABC经过平移后,使点A与点A′(-1,4)重合.
如图,△ABC经过平移后,使点A与点A′(-1,4)重合. 如图,∠BAF=40°,∠ACE=130°,CE⊥CD.问CD∥AB吗?为什么?
如图,∠BAF=40°,∠ACE=130°,CE⊥CD.问CD∥AB吗?为什么?