题目内容
2.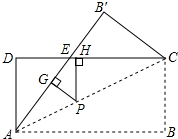 如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点B′的位置,AB′与CD交于点E.
如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点B′的位置,AB′与CD交于点E.(1)求证:△AED≌△CEB′;
(2)若P为线段AC上的任意一点,PG⊥AE于G,PH⊥EC于H,则请你证明PH•AP=PG•CP.
分析 (1)由折叠的性质知,CB′=BC=AD,∠B=∠B′=∠D=90°,∠B′EC=DEA,则由AAS得到△AED≌△CEB′;
(2)PG⊥AE于G,PH⊥EC于H,则∠PGA=∠PHC=90°,根据折叠的性质和矩形的性质易证∠PAG=∠PCH,则△PGA∽△PHC,所以PH•AP=PG•CP.
解答 解:(1)△AED≌△CEB′
证明:∵四边形ABCD为矩形,
∴B′C=BC=AD,∠B′=∠B=∠D=90°,
又∵∠B′EC=∠DEA,
∴△AED≌△CEB′;
(2)∵四边形ABCD为矩形,
∴CD∥AB
∴∠DCA=∠BAC
根据折叠的性质∠EAC=∠BAC
∴∠PAG=∠PCH,
∵PG⊥AE于G,PH⊥EC于H,
∴∠PGA=∠PHC=90°,
∴△PGA∽△PHC,
∴$\frac{PA}{PC}=\frac{PG}{PH}$
∴PH•AP=PG•CP.
点评 本题主要考查了全等三角形的判定与性质、矩形的性质、折叠的性质以及相似三角形的判定与性质,熟悉折叠图形的特点,熟练运用全等和相似的性质和判定是解决问题的关键.

练习册系列答案
相关题目
12.把ax2-4ay2分解因式正确的是( )
| A. | a(x+2y)(x-2y) | B. | a(x-2y)2 | C. | a(x-4y)2 | D. | a(x+4y)(x-4y) |
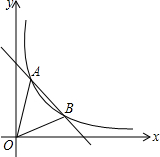 如图,已知A(-1,2),B(m,1)是一次函数y=-x+b的图象和反比例函数y=$\frac{2}{x}$(x>0)的图象的两个交点,连结AO,BO.
如图,已知A(-1,2),B(m,1)是一次函数y=-x+b的图象和反比例函数y=$\frac{2}{x}$(x>0)的图象的两个交点,连结AO,BO.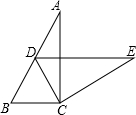 如图,在Rt△ABC中,∠ACB=90°,∠A=32°,将△ABC绕点C按顺时针方向旋转后
如图,在Rt△ABC中,∠ACB=90°,∠A=32°,将△ABC绕点C按顺时针方向旋转后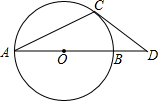 如图,AB是⊙O的直径,OA=1,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若BD=$\sqrt{2}$-1,则∠ACD=112.5°.
如图,AB是⊙O的直径,OA=1,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若BD=$\sqrt{2}$-1,则∠ACD=112.5°.