题目内容
13.若关于x的方程(m+3)${x}^{{m}^{2}-7}$+(m-5)x+5=0是一元二次方程,试求代数式$\frac{5m+6}{m+4}$的值.分析 根据一元二次方程的定义得到m2-7=2且m+3≠0,依此可以求得m的值,然后将其代入所求的代数式进行求值即可.
解答 解:∵关于x的方程(m+3)${x}^{{m}^{2}-7}$+(m-5)x+5=0是一元二次方程,
∴m2-7=2且m+3≠0,
解得m=3,
∴$\frac{5m+6}{m+4}$=$\frac{5×3+6}{3+4}$=3,即$\frac{5m+6}{m+4}$=3.
点评 本题考查了一元二次方程的定义.只有一个未知数且未知数最高次数为2的整式方程叫做一元二次方程,一般形式是ax2+bx+c=0(且a≠0).特别要注意a≠0的条件.这是在做题过程中容易忽视的知识点.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
5. 如图,四个小正方形拼成的大正方形,A、B、O是小正方形的顶点,P是以OA为半径的⊙O上的点,且位于右上方的小正方形内,则∠APB等于( )
如图,四个小正方形拼成的大正方形,A、B、O是小正方形的顶点,P是以OA为半径的⊙O上的点,且位于右上方的小正方形内,则∠APB等于( )
 如图,四个小正方形拼成的大正方形,A、B、O是小正方形的顶点,P是以OA为半径的⊙O上的点,且位于右上方的小正方形内,则∠APB等于( )
如图,四个小正方形拼成的大正方形,A、B、O是小正方形的顶点,P是以OA为半径的⊙O上的点,且位于右上方的小正方形内,则∠APB等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
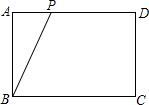 已知矩形ABCD中,AB=3cm,BC=4cm,一个动点P以1cm/s的速度从A点出发,沿AD,DC运动到C点,在这一过程中,运动时间x(s),P离D的距离为y(cm).
已知矩形ABCD中,AB=3cm,BC=4cm,一个动点P以1cm/s的速度从A点出发,沿AD,DC运动到C点,在这一过程中,运动时间x(s),P离D的距离为y(cm).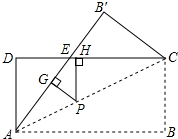 如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点B′的位置,AB′与CD交于点E.
如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点B′的位置,AB′与CD交于点E.