题目内容
17. 如图,在Rt△ABC中,∠ACB=90°,∠A=32°,将△ABC绕点C按顺时针方向旋转后
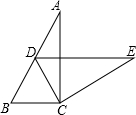
如图,在Rt△ABC中,∠ACB=90°,∠A=32°,将△ABC绕点C按顺时针方向旋转后得到△EDC,此时点D在AB边上,则旋转角的大小为64度.
分析 先利用互余计算出∠B=58°,再根据旋转的性质得CB=CD,旋转角等于∠BCD,根据等腰三角形的性质得∠B=∠BDC=58°,然后根据三角形内角和定理计算∠BCD即可.
解答 解:∵∠ACB=90°,∠A=32°,
∴∠B=90°-32°=58°,
∵△ABC绕点C按顺时针方向旋转后得到△EDC,
∴CB=CD,旋转角等于∠BCD,
∴∠B=∠BDC=58°,
∴∠BCD=180°-58°-58°=64°,
即旋转角为64°.
故答案为64.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.

练习册系列答案
相关题目
5. 如图,四个小正方形拼成的大正方形,A、B、O是小正方形的顶点,P是以OA为半径的⊙O上的点,且位于右上方的小正方形内,则∠APB等于( )
如图,四个小正方形拼成的大正方形,A、B、O是小正方形的顶点,P是以OA为半径的⊙O上的点,且位于右上方的小正方形内,则∠APB等于( )
 如图,四个小正方形拼成的大正方形,A、B、O是小正方形的顶点,P是以OA为半径的⊙O上的点,且位于右上方的小正方形内,则∠APB等于( )
如图,四个小正方形拼成的大正方形,A、B、O是小正方形的顶点,P是以OA为半径的⊙O上的点,且位于右上方的小正方形内,则∠APB等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
12.若关于x的方程$\frac{ax-1}{2-x}=\frac{3}{4}$无解,则a的值为( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | $-\frac{3}{4}$ | D. | $\frac{1}{2}$或$-\frac{3}{4}$ |
9.230 000用科学记数法表示应为( )
| A. | 0.23×105 | B. | 23×104 | C. | 2.3×105 | D. | 2.3×104 |
6.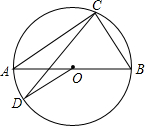 如图,AB是⊙O的直径,C、D是⊙O上的两点,分别连接AC、BC、CD、OD.若∠DOB=140°,则∠ACD=( )
如图,AB是⊙O的直径,C、D是⊙O上的两点,分别连接AC、BC、CD、OD.若∠DOB=140°,则∠ACD=( )
 如图,AB是⊙O的直径,C、D是⊙O上的两点,分别连接AC、BC、CD、OD.若∠DOB=140°,则∠ACD=( )
如图,AB是⊙O的直径,C、D是⊙O上的两点,分别连接AC、BC、CD、OD.若∠DOB=140°,则∠ACD=( )| A. | 20° | B. | 30° | C. | 40° | D. | 70° |
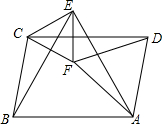 如图所示,在平行四边形ABCD中,分别以AB、AD为边作等边△ABE和等边△ADF,分别连接CE、CF和EF,则下列结论中一定成立的是①②③(把所有正确结论的序号都填在横线上).
如图所示,在平行四边形ABCD中,分别以AB、AD为边作等边△ABE和等边△ADF,分别连接CE、CF和EF,则下列结论中一定成立的是①②③(把所有正确结论的序号都填在横线上).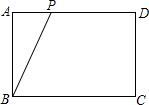 已知矩形ABCD中,AB=3cm,BC=4cm,一个动点P以1cm/s的速度从A点出发,沿AD,DC运动到C点,在这一过程中,运动时间x(s),P离D的距离为y(cm).
已知矩形ABCD中,AB=3cm,BC=4cm,一个动点P以1cm/s的速度从A点出发,沿AD,DC运动到C点,在这一过程中,运动时间x(s),P离D的距离为y(cm).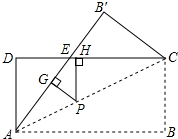 如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点B′的位置,AB′与CD交于点E.
如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点B′的位置,AB′与CD交于点E.