题目内容
16.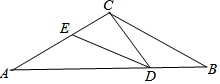 如图,在△ABC中,BC=AC,∠ACB=120°,点D在线段AB上运动(D不与A、B重合),连接CD,作∠CDE=30°,DE交线段AC于点E.
如图,在△ABC中,BC=AC,∠ACB=120°,点D在线段AB上运动(D不与A、B重合),连接CD,作∠CDE=30°,DE交线段AC于点E.(1)当DE∥BC时,△ACD的形状是直角三角形(填锐角、直角或钝角)
(2)请添加一个条件,使得△ADE≌△BCD,并说明理由.
(3)在点D运动的过程中,△CDE的形状可以是等腰三角形吗?若可以,请直接写出∠AED的度数;若不可以,请说明理由.
分析 (1)由DE∥BC,∠CDE=30°,可得∠BCD=30°,再由∠ACB=120°,即可推出∠ACD=90°,即可推出△ACD的形状为直角三角形;
(2)根据BC=AD,得到AC=AD,∠ACD=∠ADC,由已知条件即可推出∠A=∠B=30°,即可推出∠CDB=∠A+∠ACD,∠AED=∠ACD+∠CDE,再由∠A=∠CDE=30°,即可推出∠AED=∠BDC,然后通过全等三角形的判定定理“AAS”即可推出结论;
(3)分EC=DE、CD=DE、EC=CD三种情况,根据等腰三角形的性质解答即可.
解答 解:(1)∵DE∥BC,∠CDE=30°,
∴∠BCD=30°,
∵∠ACB=120°,
∴∠ACD=90°,
∴△ACD的形状为直角三角形,
故答案为:直角;
(2)添加条件AD=BC,
∵BC=AC,∠ACB=120°,
∴AC=AD,∠ACD=∠ADC,∠A=∠B=30°,
∵∠CDB=∠A+∠ACD,∠AED=∠ACD+∠CDE,
∴∠A=∠CDE,∠AED=∠BDC,
∴∠AED=∠BDC,
∵在△AED和△BDC中,
$\left\{\begin{array}{l}{∠A=∠B}\\{∠AED=∠BDC}\\{AD=BC}\end{array}\right.$,
∴△ADE≌△BCD;
(3)△ECD可以是等腰三角形.
理由如下:①当EC=DE时,∠CDE=∠ECD,
∴∠ECD=∠CDE=30°,
∵∠AED=∠ECD+∠CDE,
∴∠AED=60°,
②当CD=DE时,∠ECD=∠CED,
∵∠ECD+∠CED+∠CDE=180°,
∴∠CED=$\frac{180°-30°}{2}$=75°,
∴∠AED=180°-∠CED=105°,
③当EC=CD时,∠CED=∠CDE,
∠ACD=180°-∠CED-∠CDE=180°-30°-30°=120°,
∵∠ACB=120°,
∴此时,点D与点B重合,不合题意.
综上,△ECD可以是等腰三角形,此时∠AED的度数为60°或105.
点评 本题考查的是三角形的有关知识,掌握直角三角形的判定定理、全等三角形的判定定理和性质定理、等腰三角形的性质是解题的关键.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 没有实数根 | D. | 不能确定 |
| A. | 过两点有无数条直线 | B. | 连结两点的线段叫做两点的距离 | ||
| C. | 两点之间,线段最短 | D. | AB=BC,则点B是线段AC的中点 |
| A. | 4×103千米 | B. | 6×103千米 | C. | 8×103千米 | D. | 6×104千米 |
