题目内容
16. 如图,⊙O的直径为10,OC⊥AB于点D,CD=3,P为⊙O上一点,连接PC,则tan∠APC=$\frac{\sqrt{21}}{7}$.
如图,⊙O的直径为10,OC⊥AB于点D,CD=3,P为⊙O上一点,连接PC,则tan∠APC=$\frac{\sqrt{21}}{7}$.
分析 连接BE、OB,由垂径定理得出$\widehat{AC}=\widehat{BC}$,∠ODB=90°,由圆周角定理得出∠APC=∠E,求出DE=CE-CD=7,OC=OB=5,得出OD=2,由勾股定理求出BD,tan∠APC=tan∠E=$\frac{BD}{DE}$=$\frac{\sqrt{21}}{7}$即可.
解答 解:如图所示:连接BE、OB, ∵OC⊥AB,
∵OC⊥AB,
∴$\widehat{AC}=\widehat{BC}$,∠ODB=90°,
∴∠APC=∠E,
∵CE是⊙O的直径,
∴CE=10,
∴DE=CE-CD=7,OC=OB=5,
∴OD=2,
由勾股定理得:BD=$\sqrt{{5}^{2}-{2}^{2}}$=$\sqrt{21}$,
∴tan∠APC=tan∠E=$\frac{BD}{DE}$=$\frac{\sqrt{21}}{7}$;
故答案为:$\frac{\sqrt{21}}{7}$.
点评 本题考查了垂径定理、圆周角定理、勾股定理、三角函数;熟练掌握圆周角定理和垂径定理,由圆周角定理得出∠APC=∠E是解决问题的关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
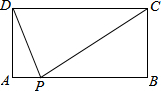 如图,矩形ABCD中,AB=5,AD=2,点P是AB边上不与A、B重合的点,要使△DPA与△PCB相似(相似比不为1),需加一个条件,这个条件是∠DPC=90°.
如图,矩形ABCD中,AB=5,AD=2,点P是AB边上不与A、B重合的点,要使△DPA与△PCB相似(相似比不为1),需加一个条件,这个条件是∠DPC=90°.